In order to build a longitudinal data set, data of adult finches Geospiza fortis living on one of the Galapagos islands were collected. The beak shape data collected between 1971-2001 are shown in the graph.
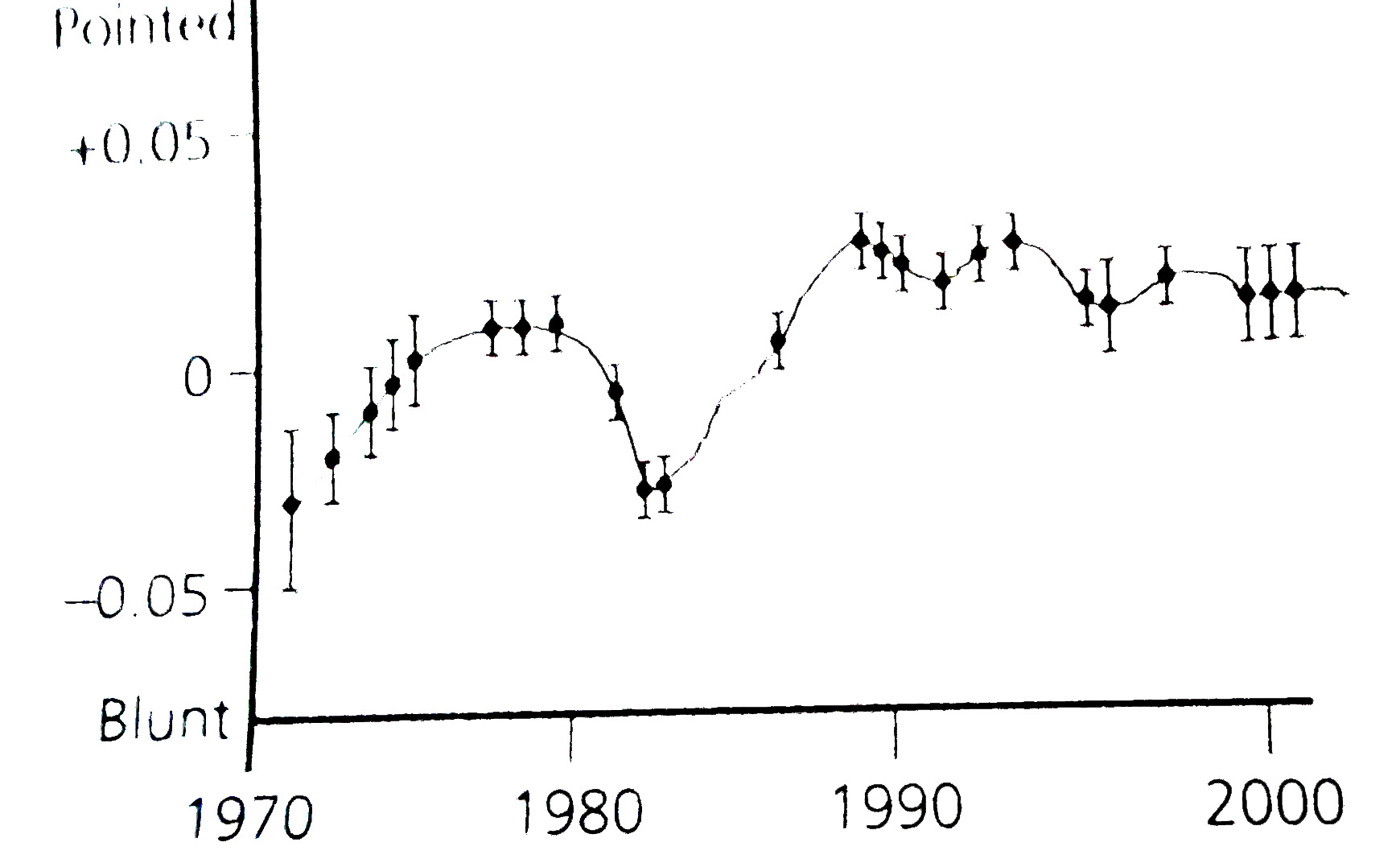
Study the graph and select the correct statement.
In order to build a longitudinal data set, data of adult finches Geospiza fortis living on one of the Galapagos islands were collected. The beak shape data collected between 1971-2001 are shown in the graph.
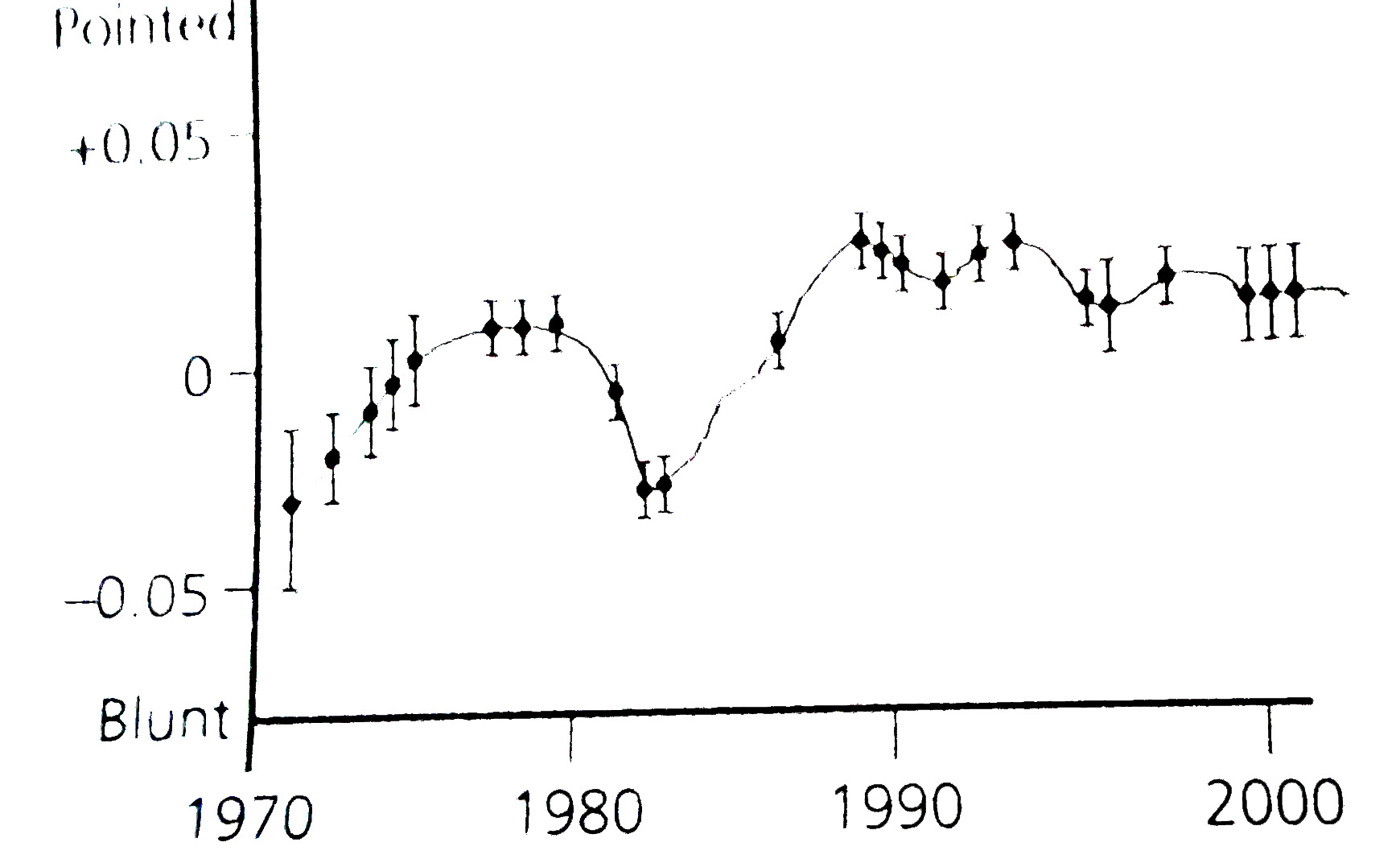
Study the graph and select the correct statement.
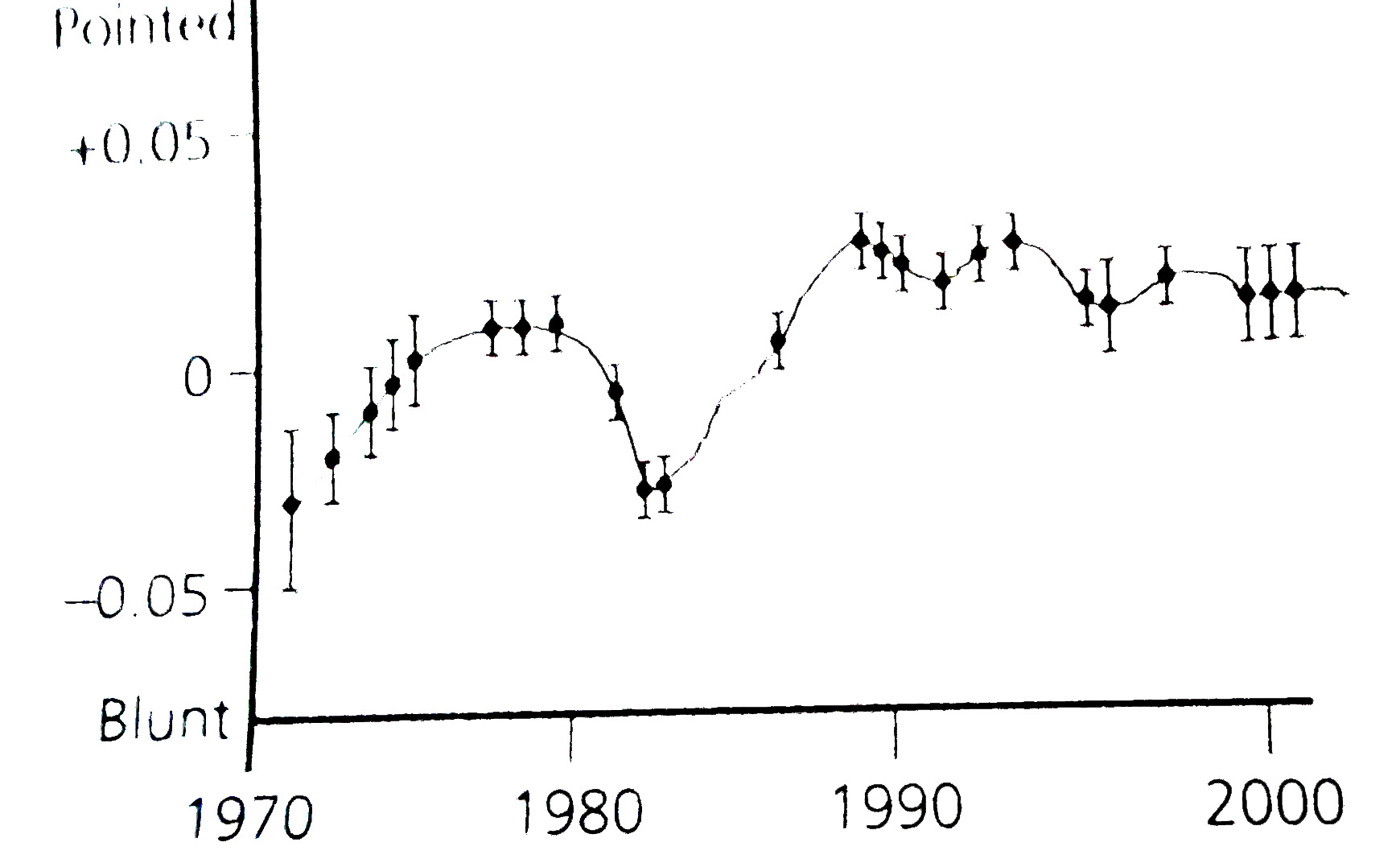
Study the graph and select the correct statement.
A
The fluctuating direction in the beak shape is most probable due to change in the environment.
B
The graph as a whole does not indicate evolutionary change in the beak shape as the time interval is too small and evolution requires thousands of years to occur.
C
The graph indicates that the beak shape may lead to convergent evolutin in the finches of Galapagos inslands.
D
The change in any phenotypic character requires selection to alter the expression of large number of geries in coordinated fashion. Henc,e it is unlikely that change in the beak shape depicted in the graph is a result of evolution.
Text Solution
Verified by Experts
The correct Answer is:
A
The diversity in beak shape is most probable due to changes in environment which lead to natural selection and gene flow among species. The graph does indicate evolutionary change. It has been shown that evolution can occur with surprising speed, as fast as those resulting from artifical selection. The selection in case of finches was strong and the populations evolved in a matter or generations. The Galapagos finches afford an excellent example of adaptive radiation. It is assumed taht a stock of ancestral finches reached the islands from the mainland and then in the absence of much competition, evolved to fill many of the empty ecological niches. There a change in a phenotypic character can be attributed to alteration in the expression of one to several genes. Thus the change in beak shape can be atributed to evolution.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Direction : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends on the properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} Which object would first acquire half of their respective terminal speed in minimum time from start of the motion of all were released simultaneously ?
Direction : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} If buoyant force were also taken into account then value of terminal speed would have
Direction : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} Which object has greatest terminal speed in the liquid ?
Direction : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} If an object of mass 2 kg and constant b = 4 (N-s)/(m) has terminal speed v_(T) in a liquid then time required to reach 0.63 v_(T) from start of the motion is :
Direction : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} At the start of motion when object is released in the liquid, its acceleration is :
Direction : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g = 10.00 m//s^(2) ) :
Study following statements regarding the preparation of herbarium sheets. (i) Plant should be collected in flowering stage. (ii) Every detail regarding the plant such sa locality, ecological conditions, vegetative and floral characters, etc. should be noted. (iii) Plants are evenly pressed by unfolding all the plant parts between blotting papers (or newspapers) with the help of plant pressers. (iv) Blotting papers need not be changed until the plant gets dried. (v) After drying, the plant specimen is carefully mounted/pasted on the herbarium sheets. (vi) The herbarium sheet is labelled on the lower right hand corner representing the number of plant specimen, data of collection, etc. Which of the above statements is/are correct ?
Between 1985 and 2003, data were collected every three years on the amount of plastic produced annually in the United States, in billions of pounds. The graph below shows the data and a line of best fit. The equation of the line of best fit is y = 3.39x + 46.89, where x is the number of years since 1985 and y is the amount of plastic produced annually, in billions of pounds. Which of the following is closest to the percent increase in the billions of pounds of plastic produced in the United States from 2000 to 2003?
Read the following statements with one or two blanks in each one of them. (i) A genus containing more than one species is called ______ genus, e.g., _______ . (ii) _______ is a collection of dried, pressed and preserved plants mounted on _________ sheets, properly labelled, systematically arranged and available for reference study. (iii) Living fossils are ancient organisms persisting in modern times _______ gradual morphological changes. (iv) A ________ is compreshensive treatise of a taxonomic group, generally a genus or a family, providing all taxonomic data related to that group. Which of the following correctly fills any two of the above statements ?
NCERT FINGERTIPS ENGLISH-EVOLUTION-All Questions
- Homo sapiens arose during which epoch?
Text Solution
|
- Study of human evolution is called
Text Solution
|
- In order to build a longitudinal data set, data of adult finches Geosp...
Text Solution
|
- The following summaries describe some published research results. Re...
Text Solution
|
- Study the charactristics of a population represented in the graphs bel...
Text Solution
|
- Study the charactristics of a population represented in the graphs bel...
Text Solution
|
- Following table shows data on amino acid substitution in the alpha cha...
Text Solution
|
- In a long term experiment of a population of Drosophila melnogaster, t...
Text Solution
|
- In a large, randomly mating population, only one person in 10,000 is a...
Text Solution
|
- Which of the following is used an atomospheric pollution indicator?
Text Solution
|
- The theory of spontaneous generation stated that
Text Solution
|
- Animal husbandry and plant breeding programmers are the examples of
Text Solution
|
- Palaentological evidences for evolution refer to the
Text Solution
|
- The bones of forelimbs of whale, bat, cheetah and man are similar in s...
Text Solution
|
- Analogous organs arise due to
Text Solution
|
- (pq)^(2)+2pq+q^(2)=1 represents an equation used in
Text Solution
|
- Appearance of antibiotic-resistant bacteria is an example of
Text Solution
|
- Evolution of life shows that life hard a trent of moving from
Text Solution
|
- Viviparity is considered to be more evolved because
Text Solution
|
- Fossils are generally found in
Text Solution
|