Home
Class 11
PHYSICS
Six point masses of mass m each are at t...

Six point masses of mass `m` each are at the vertices of a regular hexagon of side `l`. Calculate the force on any of the masses.

A

`(Gm^(2))/(l^(2))[(5)/(4)+(1)/(sqrt(3))]`

B

`(Gm^(2))/(l^(2))[(3)/(4)+(1)/(sqrt(3))]`

C

`(Gm^(2))/(l^(2))[(5)/(4)-(1)/(sqrt(3))]`

D

`(Gm^(2))/(l^(2))[(3)/(4)-(1)/(sqrt(3))]`

Text Solution

Verified by Experts

The correct Answer is:
A
(a)
From Figure,
`AC=AM+MC=2AM=2lcos30^(@)=2l(sqrt(3))/(2)=sqrt(3)l`
Similarly, `AE=sqrt(3)l`
`AD=AO+ON+ND= l sin 30^(@)+l+ lsin 30^(@)`
`lxx(1)/(2)+l+lxx(1)/(2)=2l`
`AB=AF=l`
Force on mass m at A due to mass m at B is
`F_(AB)=(Gmm)/((AB)^(2))=(Gmm)/(l^(2))` along AB
Force on mass m at A due to mass m at C is
`F_(AC)=(Gmm)/((AC)^(2))=(Gmm)/(l^(2))` along AC
Force on mass m at A due to mass m at D is
`F_(AD)=(Gmm)/((AD)^(2))=(Gmm)/(l^(2))` along AD
Force on mass m at A due to mass m at E is
`F_(AE)=(Gmm)/((AE)^(2))=(Gmm)/(l^(2))` along AE
Force on mass m at A due to mass m at F is
`F_(AF)=(Gmm)/((AF)^(2))=(Gmm)/(l^(2))` along AF
Resultant force due to `F_(AB) " and " F_(AF)` is
`F_(R_(1))=sqrt(F_(AB)^(2)+F_(AF)^(2)+2F_(AB)F_(AF)cos 120^(@))`
`=sqrt(((Gm^(2))/(l^(2)))^(2)+((Gm^(2))/(l^(2)))^(2)+2((Gm^(2))/(l^(2)))((Gm^(2))/(l^(2)))(-(1)/(2)))`
`=(Gm^(2))/(l^(2))` along AD
Resultant force due to `F_(AC) " and " F_(AE)` is
`F_(R_(2))=sqrt(F_(AC)^(2)+F_(AE)^(2)+2F_(AC)F_(AE)cos 60^(@))`
`=sqrt(((Gm^(2))/(3l^(2)))^(2)+((Gm^(2))/(3l^(2)))^(2)+2((Gm^(2))/(3l^(2)))((Gm^(2))/(3l^(2)))((1)/(2)))`
`=(sqrt(3)Gm^(2))/(3l^(2))=(Gm^(2))/(sqrt(3)l^(2))` along AD ,brgt Net force on mass m along AD is
`F_(R)=F_(R_(1))+F_(R_(2))+F_(AD)=(Gm^(2))/(l^(2))+(Gm^(2))/(sqrt(3)l^(2))+(Gm^(2))/(4l^(2))`
`=(Gm^(2))/(l^(2))[1+(1)/(sqrt(3))+(1)/(4)]=(Gm^(2))/(l^(2))[(5)/(4)+(1)/(sqrt(3))]`
Promotional Banner

Topper's Solved these Questions

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise The Gravitational constant|8 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Acceleration due to gravity below and above the surface of earth|8 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 Videos

  • KINETIC THEORY

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|10 Videos

Similar Questions

Explore conceptually related problems

Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure). Find the magnitude of electric field at the centre of regular hexagon.

Three masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?

Five point charge ( +q each) are placed at the five vertices of a regular hexagon of side 2a .what is the magnitude of the net electric field at the centre of the hexazon?

Five point masses m each are kept at five vertices of a regular pentagon. Distance of center of pentagon from any one of the vertice is 'a'. Find gravitational potential and filed strength at center.

Three equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)

Four point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon. .

Three identical point objects each of mass m are placed at the vertices of an equilateral triange of side l . What is the gravitational potential at the centre of the equilateral triangle due to the point masses?

Six point charges are kept at the vertices of a regular hexagon of side L and centre O, as shown in the figure. Given that K=(1)/(4piepsilon_0)(q)/(L^2) , which of the following statements(s) is (are) correct?

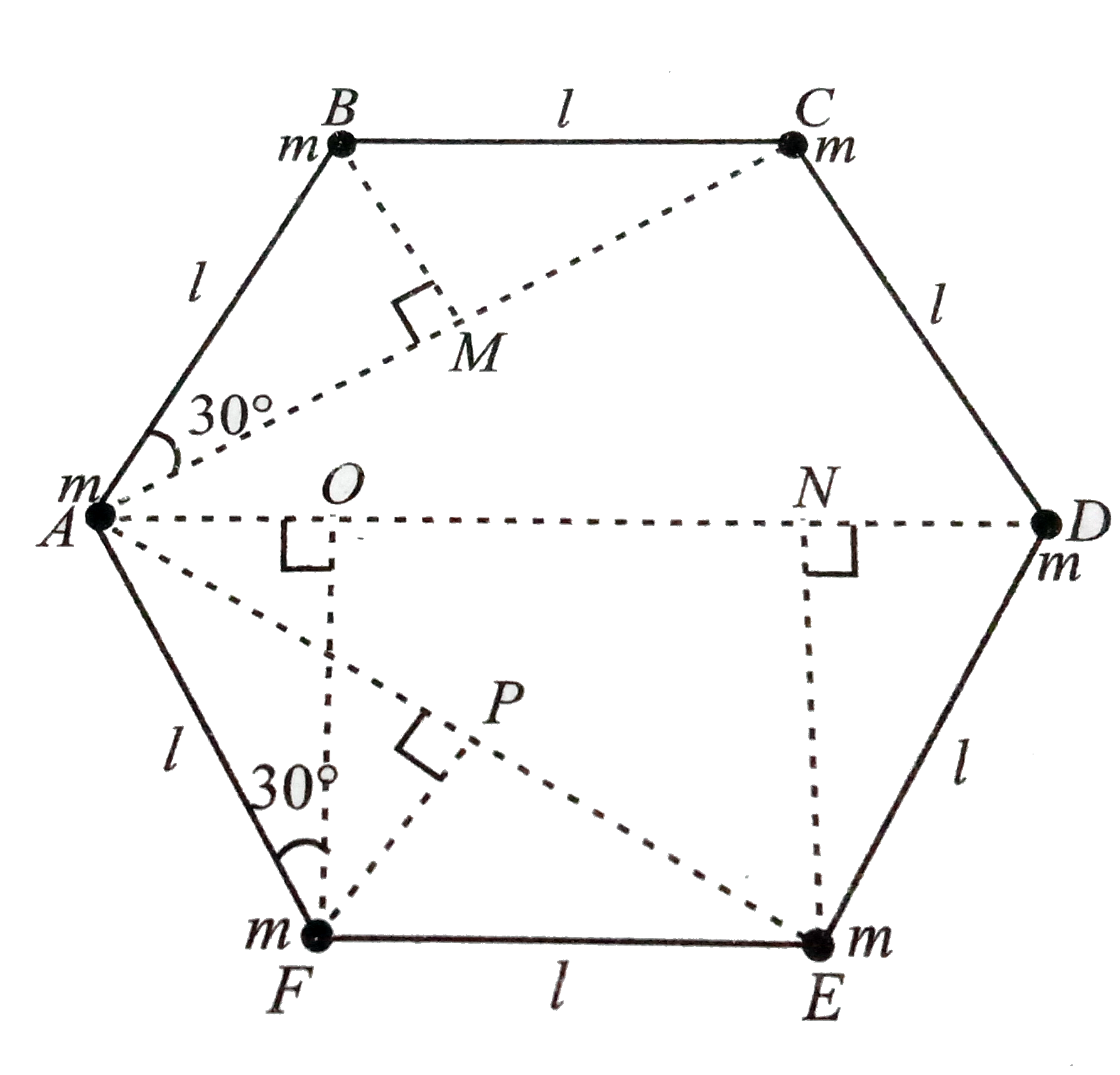
Six point charges are placed at the vertices of a regular hexagon of side a as shown. If E represents electric field and V represents electric potential at O then,

Three equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?