Home
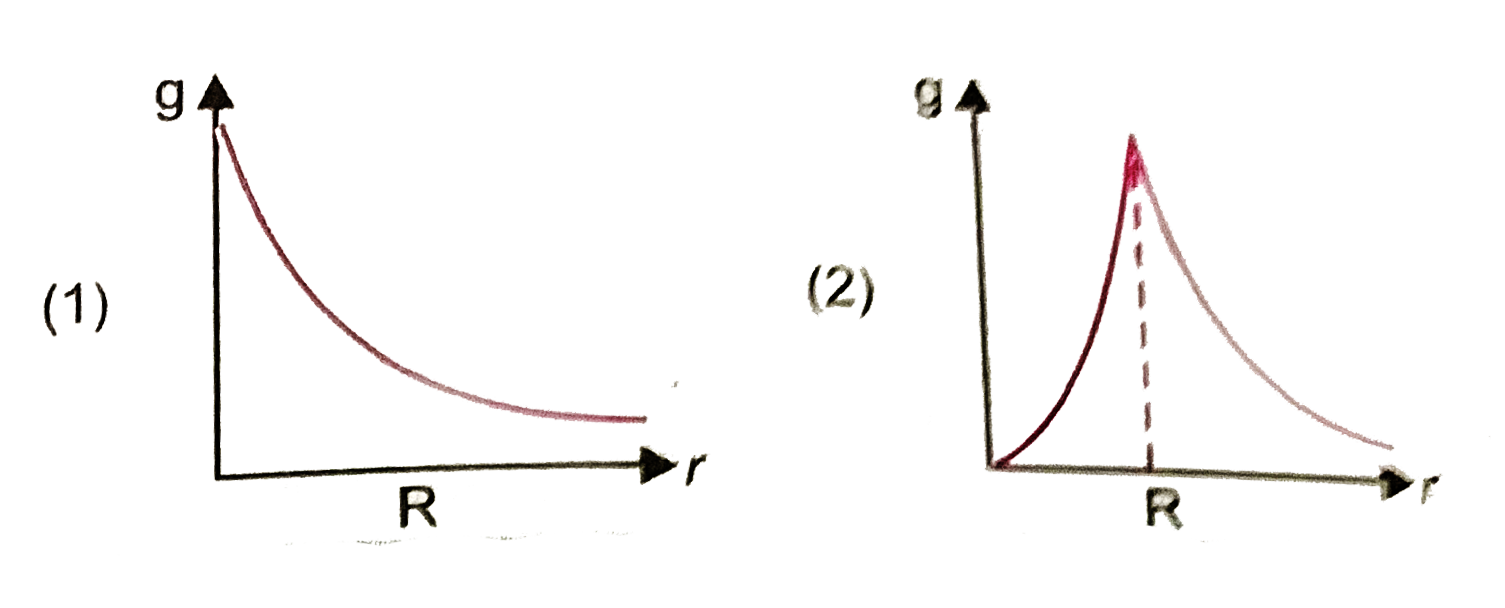
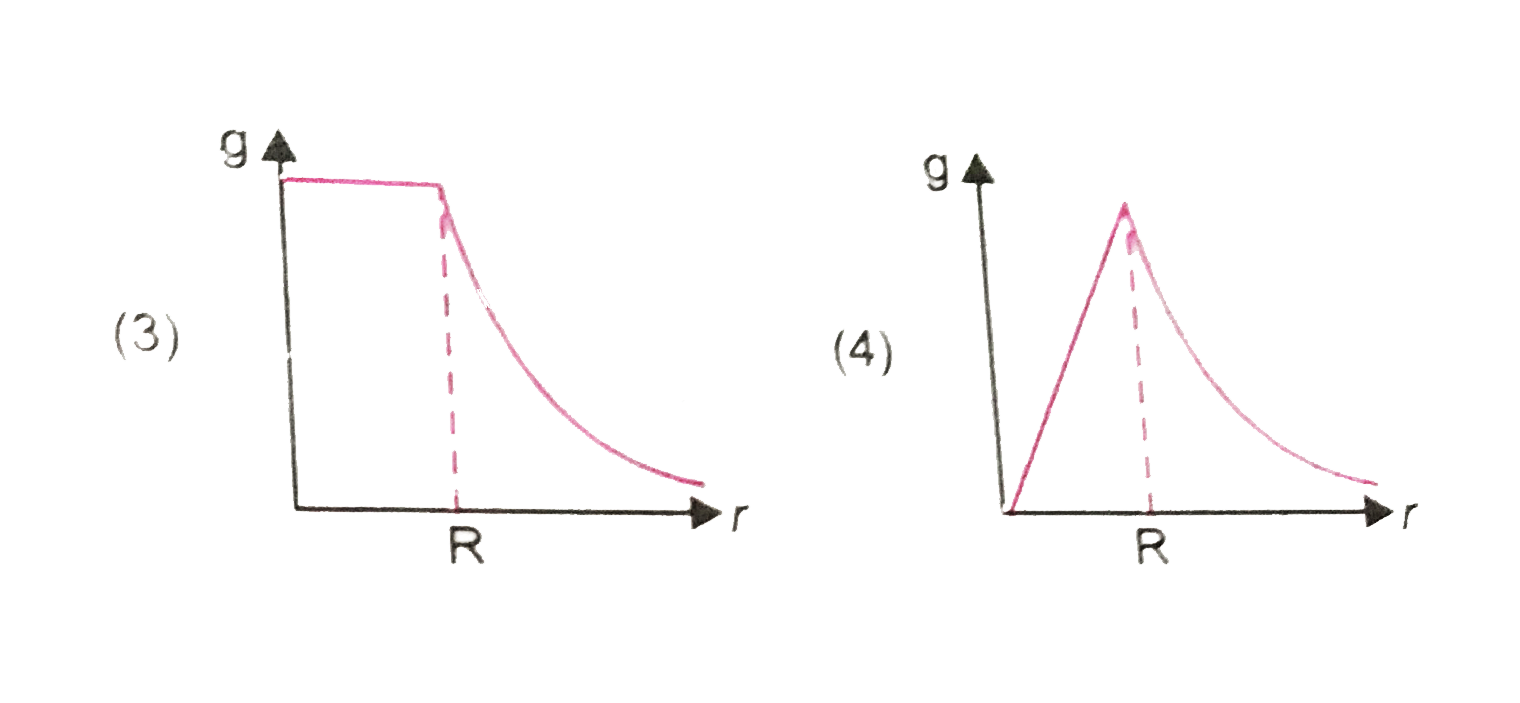
Class 11
PHYSICS
The dependence of acceleration due to gr...

The dependence of acceleration due to gravity `g` on the distance `r` from the centre of the earth, assumed to be a sphere of radius `R` of uniform density is as shown in Fig. below:


The correct figure is

A

(i)

B

(ii)

C

(iii)

D

(iv)

Text Solution

Verified by Experts

The correct Answer is:
D
(d) The acceleration due to gravity at a depth d below the surface of earth is
`g'=g(1-(d)/(R ))=g((R-d)/(R ))=g( r)/( R)` …. (i)
where R-d=r distance of location from the centre of the earth. When r=0, g'=0
From (i), `g prop r` till R=r, for which g'=g
For `r gt R, g'=(gR^(2))/((R+h)^(2))=(gR^(2))/(r^(2)) or g' prop (1)/(r^(2))`
Here, R+h=r
Therefore, the variation of g with distance r from centre of earth will be as shown in figure (4). Thus , option (d) is correct.
Promotional Banner

Topper's Solved these Questions

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Gravitational Potential energy|7 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Escape Speed|7 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise The Gravitational constant|8 Videos

  • KINETIC THEORY

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|10 Videos

Similar Questions

Explore conceptually related problems

The acceleration due to gravity at a depth R//2 below the surface of the earth is

The value of g (acceleration due to gravity) at earth's surface is 10 ms^(-2) . Its value in ms^(-2) at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is

Assuming the earth to be a sphere of uniform density, the acceleration due to gravity

The distance of geostationary satellite from the centre of the earth (radius R) is nearest to

Figure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r_(1) - r_(1)

What will be the acceleration due to gravity at a distance of 3200 km below the surface of the earth ? (Take R_(e)=6400 km)

If acceleration due to gravity at distance d [ < R ] from the centre of earth is beta , then its value at distance d above the surface of earth will be [ where R is radius of earth ]

If g_(1) and g_(2) denote acceleration due to gravity on the surface of the earth and on a planet whose mass and radius is thrice that of earth, then

Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by

If R is the radius of the earth and g the acceleration due to gravity on the earth's surface, the mean density of the earth is