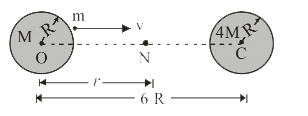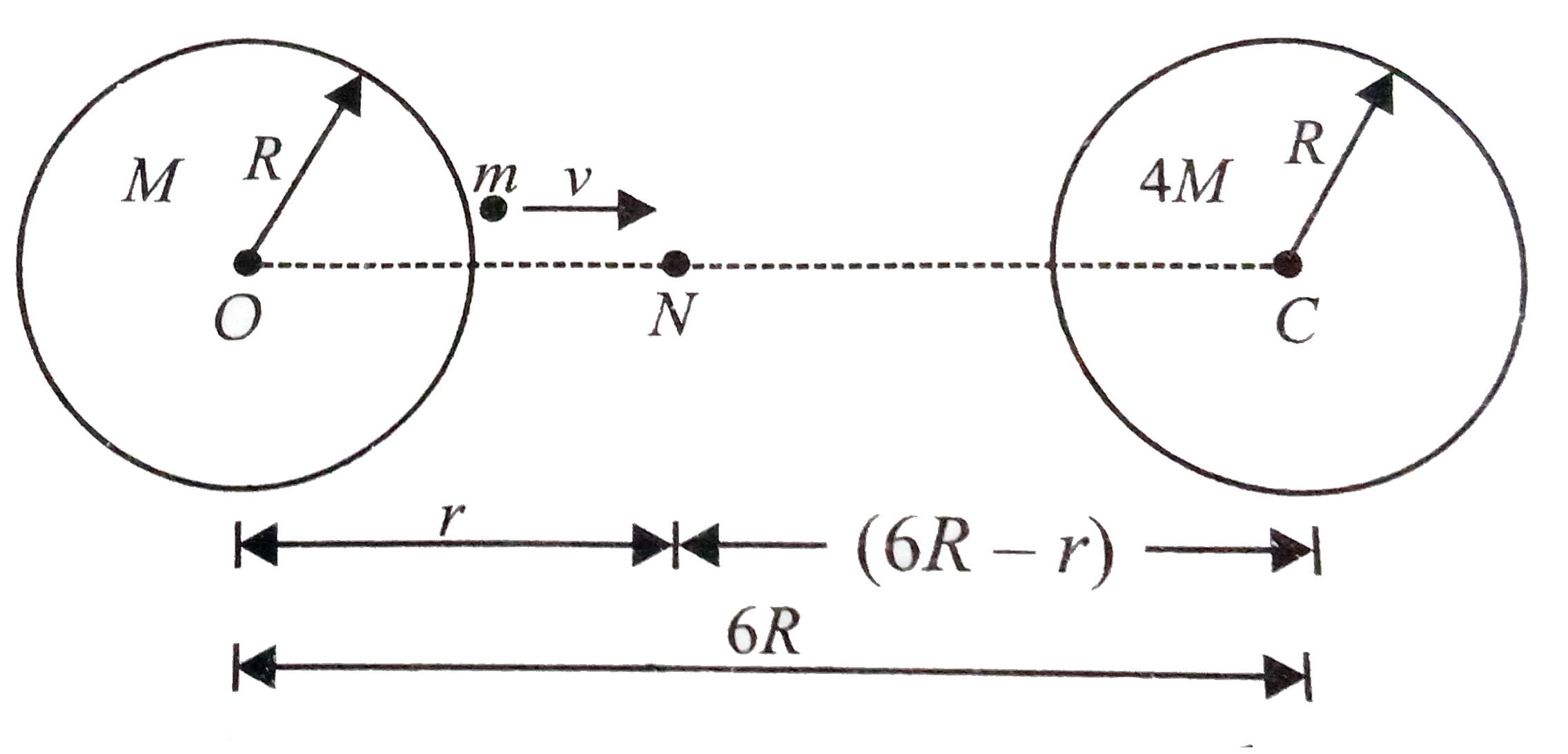Home
Class 11
PHYSICS
Two uniform solid spheres of equal radii...

Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.

A

`sqrt((4)/(5)(GM)/(R ))`

B

`sqrt((5)/(4)(GM)/(R ))`

C

`sqrt((3)/(5)(GM)/(R ))`

D

`sqrt((5)/(3)(GM)/(R ))`

Text Solution

Verified by Experts

The correct Answer is:
C
( c)
Let the projectile of mass m be fired with minimum velocity, v from the surface of sphere of mass M to reach the surface of sphere of mass 4M. Let N be neutral point at a distance r from the centre of the sphere of mass M. At neutral point N,
`(GMm)/(r^(2))=(G(4M)m)/((6 R-r)^(2))`
`(6R-r)^(2)=4r^(2)`
`6R-r=pm2r or r=2R or -6R`
The point r= -6R does not conern us. Thus, ON=r=2R
It is sufficient to project the projectile with a speed which would enable it to reach N. Thereafter, the greater gravitational pull of 4M would suffice.
The mechanical energy at the surface of M is
`E_(i)=(1)/(2)mv^(2)-(GMm)/(R )-(G (4M)m)/(5R)`
AT the neutral point, N the speed approaches zero.
`:.` The mechanical enery at N is
`E_(N)=-(GMm)/(2R)-(G(4M)m)/(4R)= -(GMm)/(2R)-(GMm)/(R )`
According to law of conservation of mechanical energy,
`E_(i)=E_(N)`
`(1P)/(2)mv^(2)-(GMm)/(R )-(4 GMm)/(5R)= - (GMm)/(2 R)-(GMm)/(R )`
`v^(2)f=(2GM)/(R)[(4)/(5)-(1)/(2)]=(3)/(5)(GM)/(R ) or v=((3)/(5)(GM)/(R))^(1//2)`
Promotional Banner

Topper's Solved these Questions

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Earth Satellite|4 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Energy of an Orbiting Satellite|15 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Gravitational Potential energy|7 Videos

  • KINETIC THEORY

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|10 Videos

Similar Questions

Explore conceptually related problems

Two uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6 R , as shows in Fig. (a) The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of teh second. Obtain an expression for the minimum speed upsilon of the projectile so that it reaches the surface of second sphere.

The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is

Two solid spherical planets of equal radii R having masses 4M and 9M their centre are separated by a distance 6R. A projectile of mass m is sent from theplanet of mass 4 M towards the heavier planet. What is the distance r of the point from the lighter planet where the gravitational force on the projectille is zero ?

A sphare of mass M and radiusR_(2) has a concentric cavity of radius R_(1) as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as (0 lerleoo) .

Three solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?

A particle of mass m is lying at the centre of a solid sphere of mass M and radius R . There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.

A cavity of radius R//2 is made inside a solid sphere of radius R . The centre of the cavity is located at a distance R//2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R//2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM//R^(2) , where M is the mass of the solide sphere]

A cavity of radius R//2 is made inside a solid sphere of radius R . The centre of the cavity is located at a distance R//2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R//2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM//R^(2) , where M is the mass of the solide sphere]

Three solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?

A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.