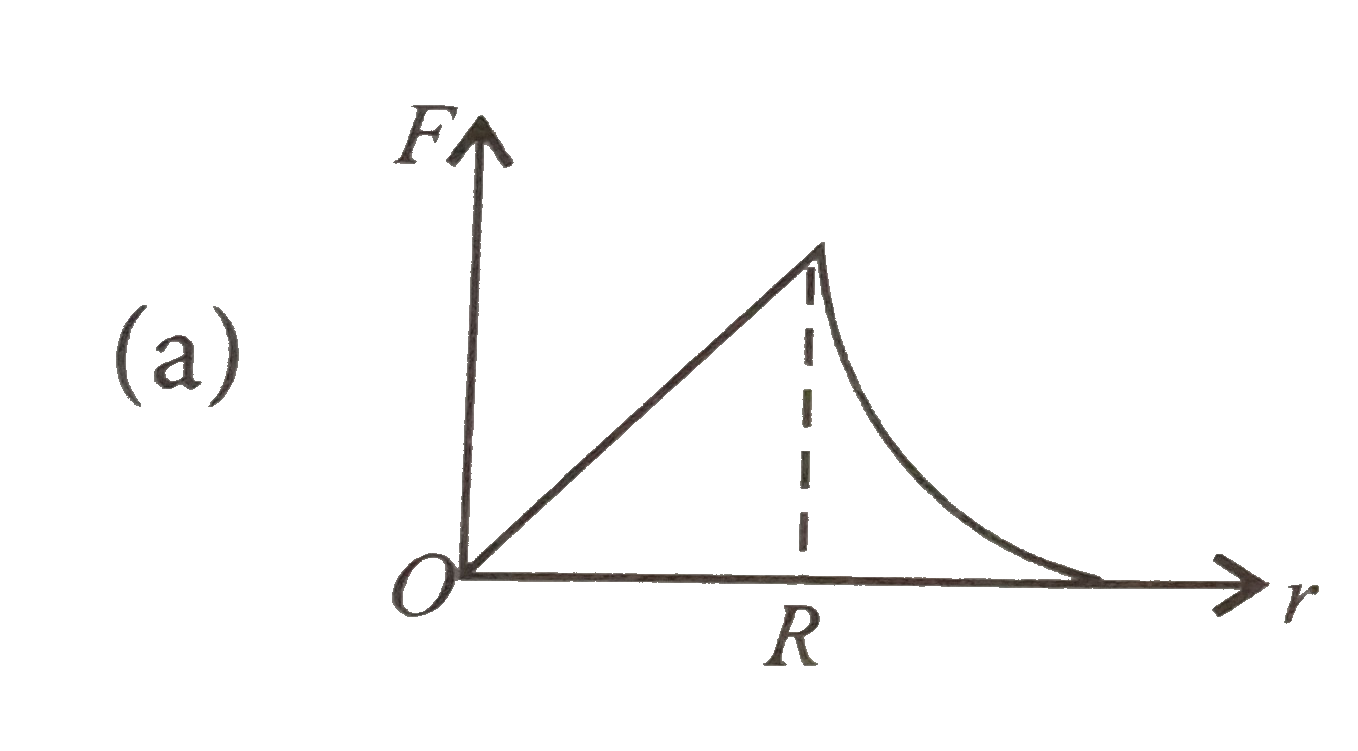
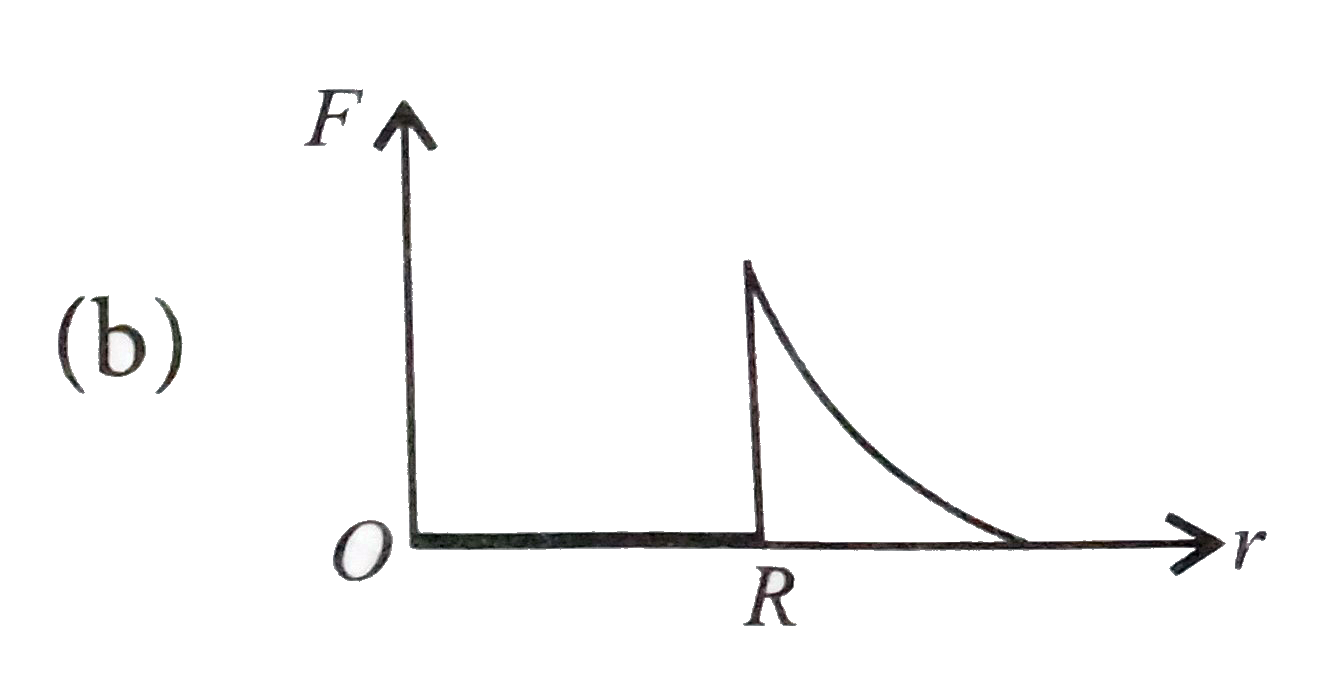
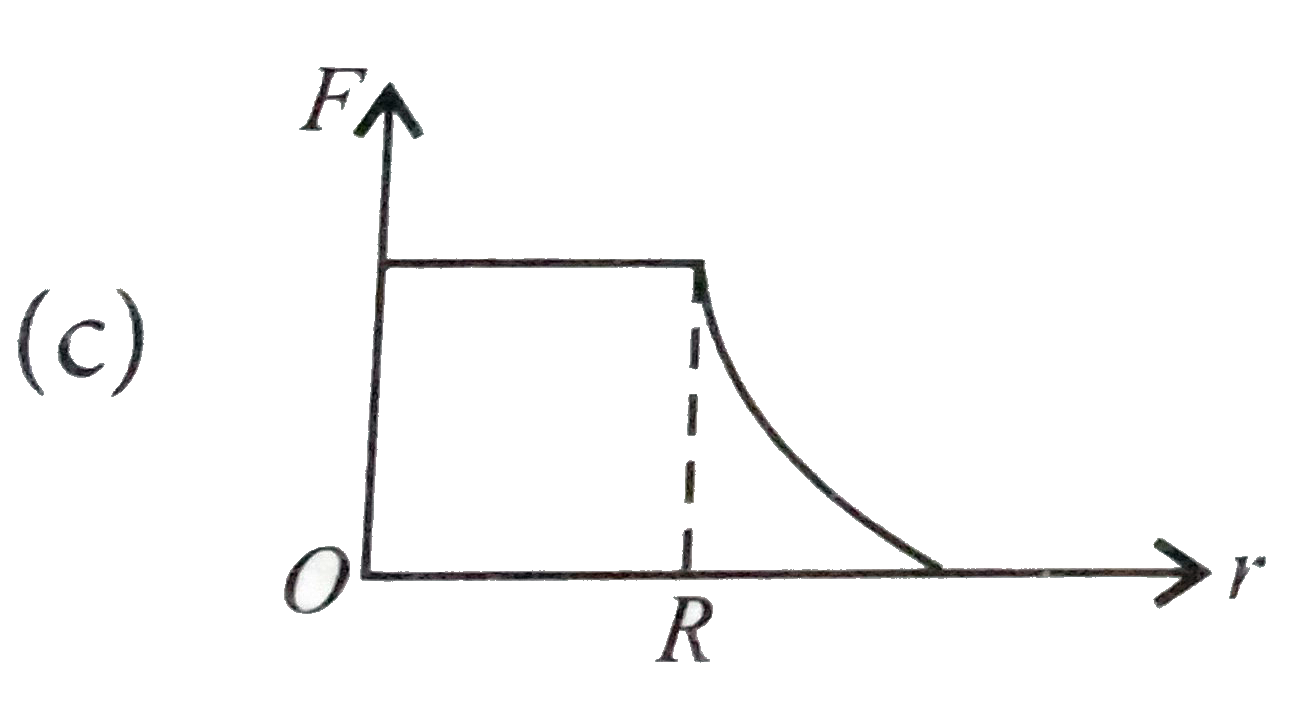
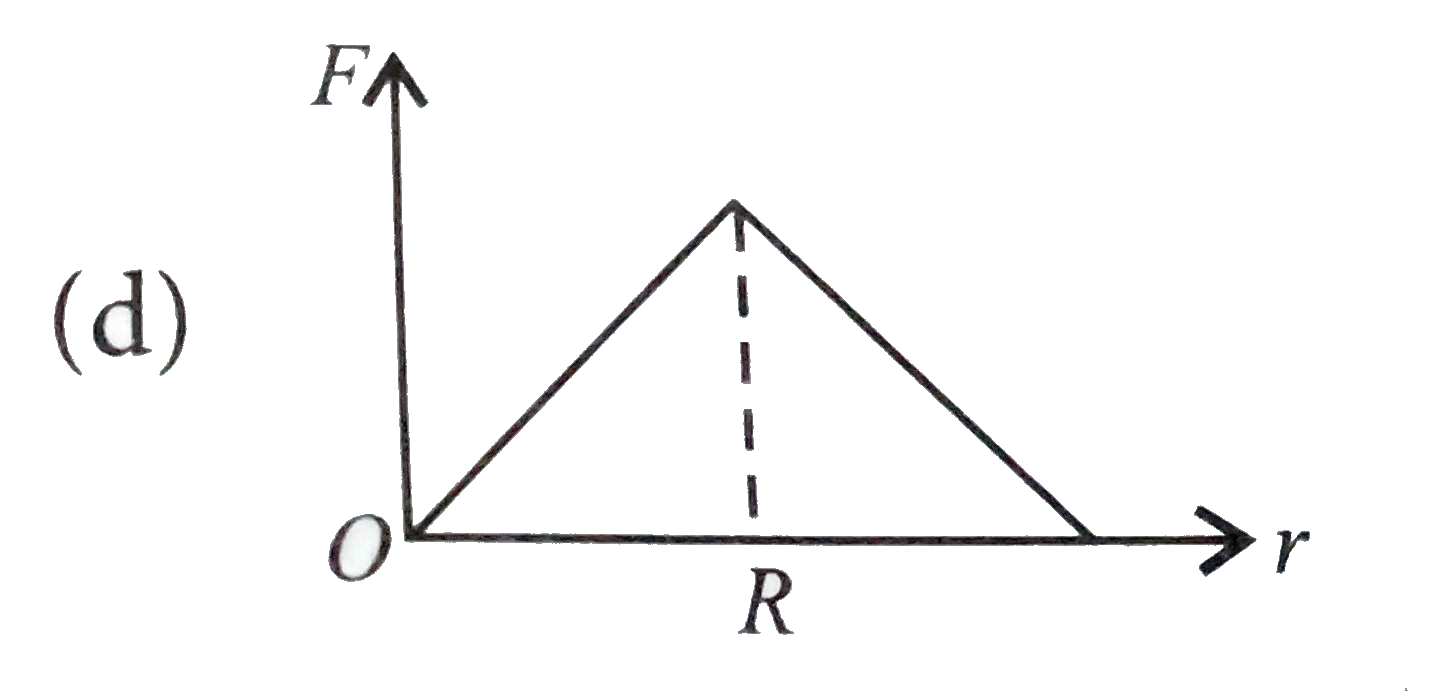
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS ENGLISH-GRAVITATION-Miscellaneous Question
- Two identical spheres of radius R made of the same material are kept a...
Text Solution
|
- The time interval between two successive noon when sun passes through ...
Text Solution
|
- Which of the following planets has two moons phobos and deimos ?
Text Solution
|
- Black Hole is
Text Solution
|
- The direction of gravitational intensity at point P of a hemispherica...
Text Solution
|
- The angular speed of rotation of the earth is
Text Solution
|
- A non-homogeneous sphere of radius R has the following density variati...
Text Solution
|
- The gravitational field intensity at a point 10,000km from the centre ...
Text Solution
|
- A satellite is revolving in a circular orbit at a height 'h' from the ...
Text Solution
|
- From a solid sphere of mass M and radius R, a spherical portion of rad...
Text Solution
|
- Which one of the following plots represents the variation of the gravi...
Text Solution
|