Home
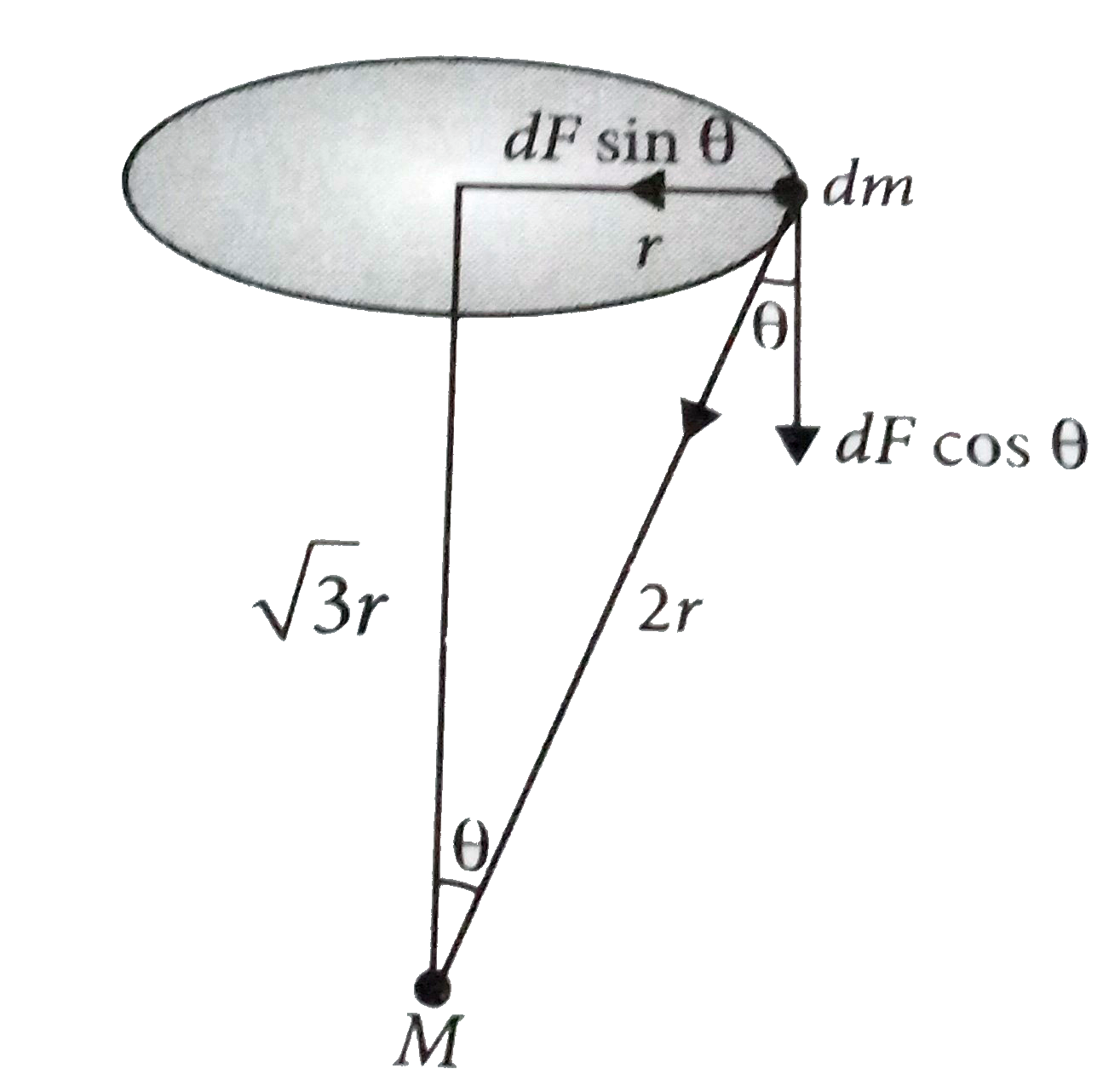
Class 11
PHYSICS
A uniform ring of mass m and radius a is...

A uniform ring of mass `m` and radius `a` is placed directly above a uniform sphere of mass `M` and of equal radius. The centre of the ring is at distance `sqrt(3)a` from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.

A

`(GMm)/(8r^(2))`

B

`(GMm)/(4r^(2))`

C

`sqrt(3)(GMm)/(8r^(2))`

D

`(GMm)/(8r^(3)sqrt(3))`

Text Solution

Verified by Experts

The correct Answer is:
C
( c) `dF=G(Mdm)/(4r^(2))`
`F=sumdFcos theta`
`=sum(GMdm)/(4r^(2)) cos theta`
`=(GM)/(4r^(2))xx(sqrt(3)r)/(2r)sumdm`
`=(sqrt(3)GMm)/(8r^(2))`
Promotional Banner

Topper's Solved these Questions

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise NCERT Exemplear Problems.|8 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Assertion & Reason Corner|15 Videos

  • GRAVITATION

    NCERT FINGERTIPS ENGLISH|Exercise Miscellaneous Question|11 Videos

  • KINETIC THEORY

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|10 Videos

Similar Questions

Explore conceptually related problems

A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance sqrt3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.

A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance sqrt3 a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.

For a uniform ring of mass M and radius R at its centre

The figure represents a solid uniform sphere of mass M and radius R . A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is

A uniform ring of mass m is lying at a distance sqrt(3) a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .

A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R . The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B .

A circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance sqrt(3)a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is

A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.

A cavity of radius R//2 is made inside a solid sphere of radius R . The centre of the cavity is located at a distance R//2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R//2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM//R^(2) , where M is the mass of the solide sphere]