Home
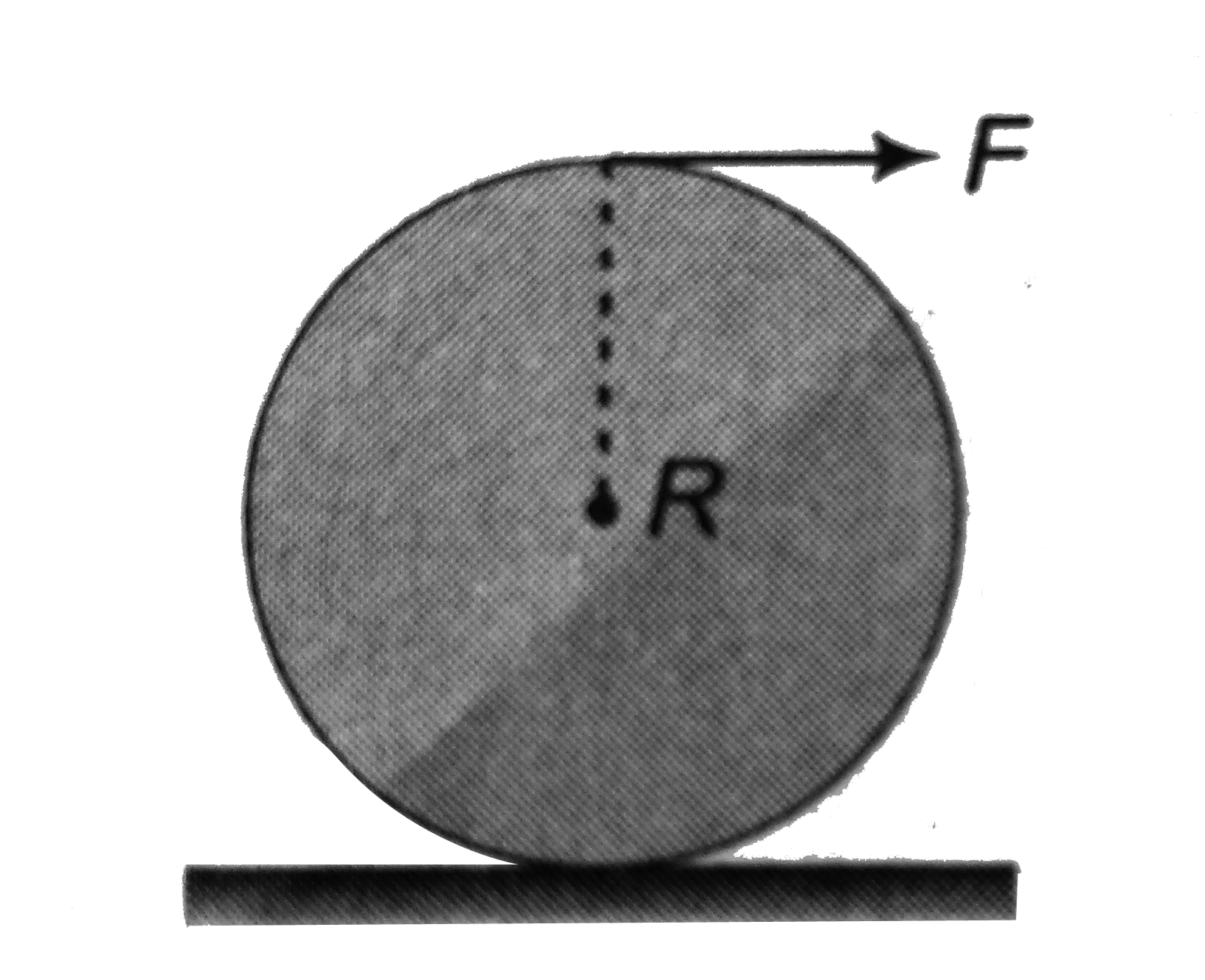
Class 11
PHYSICS
A tangential force F acts at the top of ...


A tangential force `F` acts at the top of a thin spherical shell of mass `m` and radius `R`. Find the acceleration of the shell if it rolls without slipping.

A

a. Acceleration of disc = 2F/3m

B

b. Friction force between disc and surface = 2F/3

C

c. Acceleration of disc = 6F/5m

D

d. Friction force between disc and surface is F/3

Text Solution

Verified by Experts

The correct Answer is:
d
Equation regarding translatory motion
F+f=ma……………(i)
Equation regarding rotational motion
`FR-fR = (mR^(2))/(2) a/R`…………..(ii)
From equation (i) and (ii)
`2F = (3"ma")/(2)` or `a=(4F)/(3m)`
Also, `F+f = (m4F)/(3m)`
`f=4/3F-F=F/3`
Promotional Banner

Topper's Solved these Questions

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS

    NCERT FINGERTIPS ENGLISH|Exercise NCER EXAMPLAR PROBLEMS|8 Videos

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS

    NCERT FINGERTIPS ENGLISH|Exercise ASSERTION AND REASON|15 Videos

  • SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS

    NCERT FINGERTIPS ENGLISH|Exercise ROLLING MOTION|16 Videos

  • PRACTICE PAPERS

    NCERT FINGERTIPS ENGLISH|Exercise All Questions|150 Videos

  • THERMAL PROPERTIES OF MATTER

    NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|10 Videos

Similar Questions

Explore conceptually related problems

Figure shows a hemispherical shell of mass M and radius R and a concentric shell of mass m and radius 3R/4.

If a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?

A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then

A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .

A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a/2 from the center.

A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a/2 from the centre.

A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a/2 from the centre.

A force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is

A body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is

A particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a .