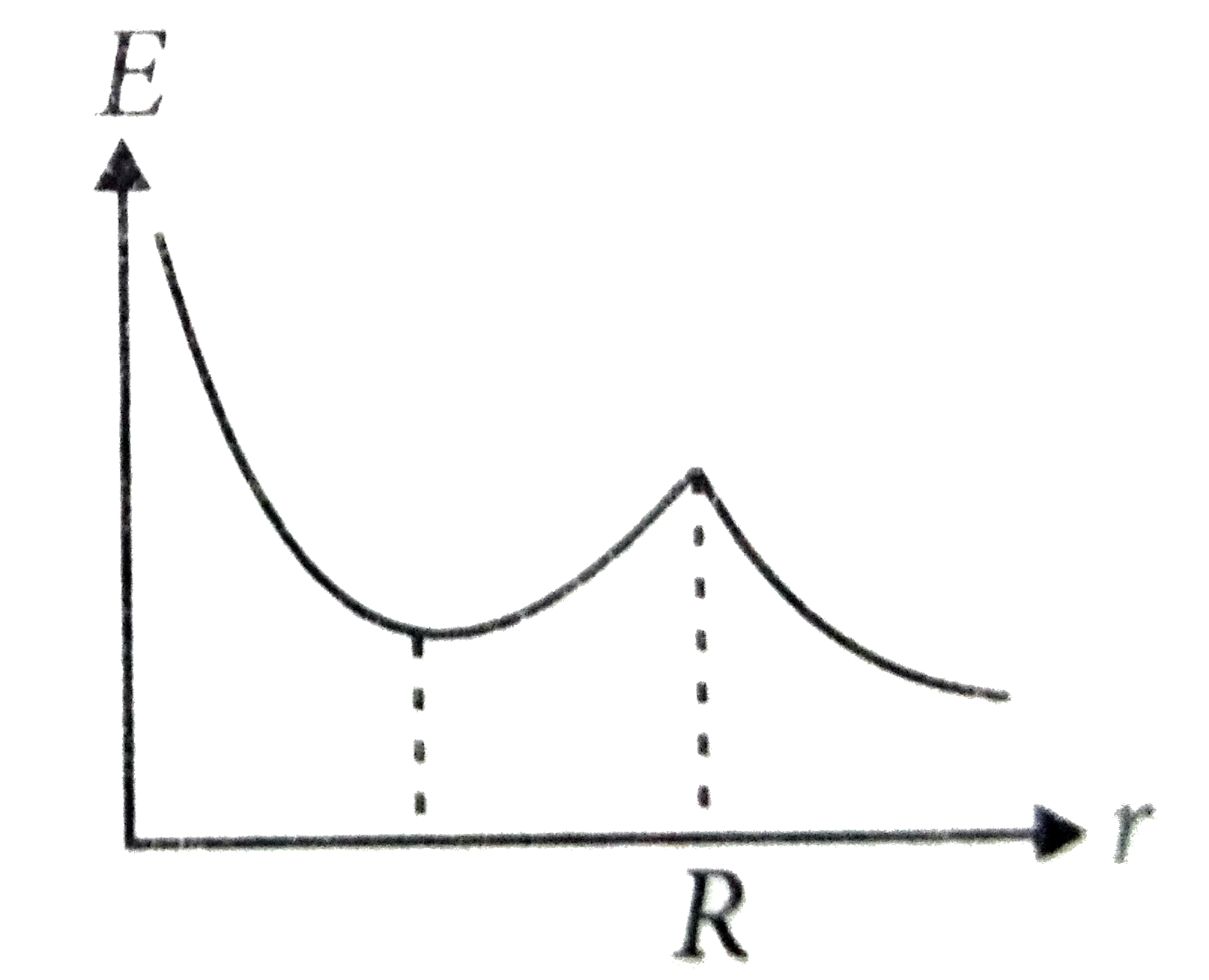
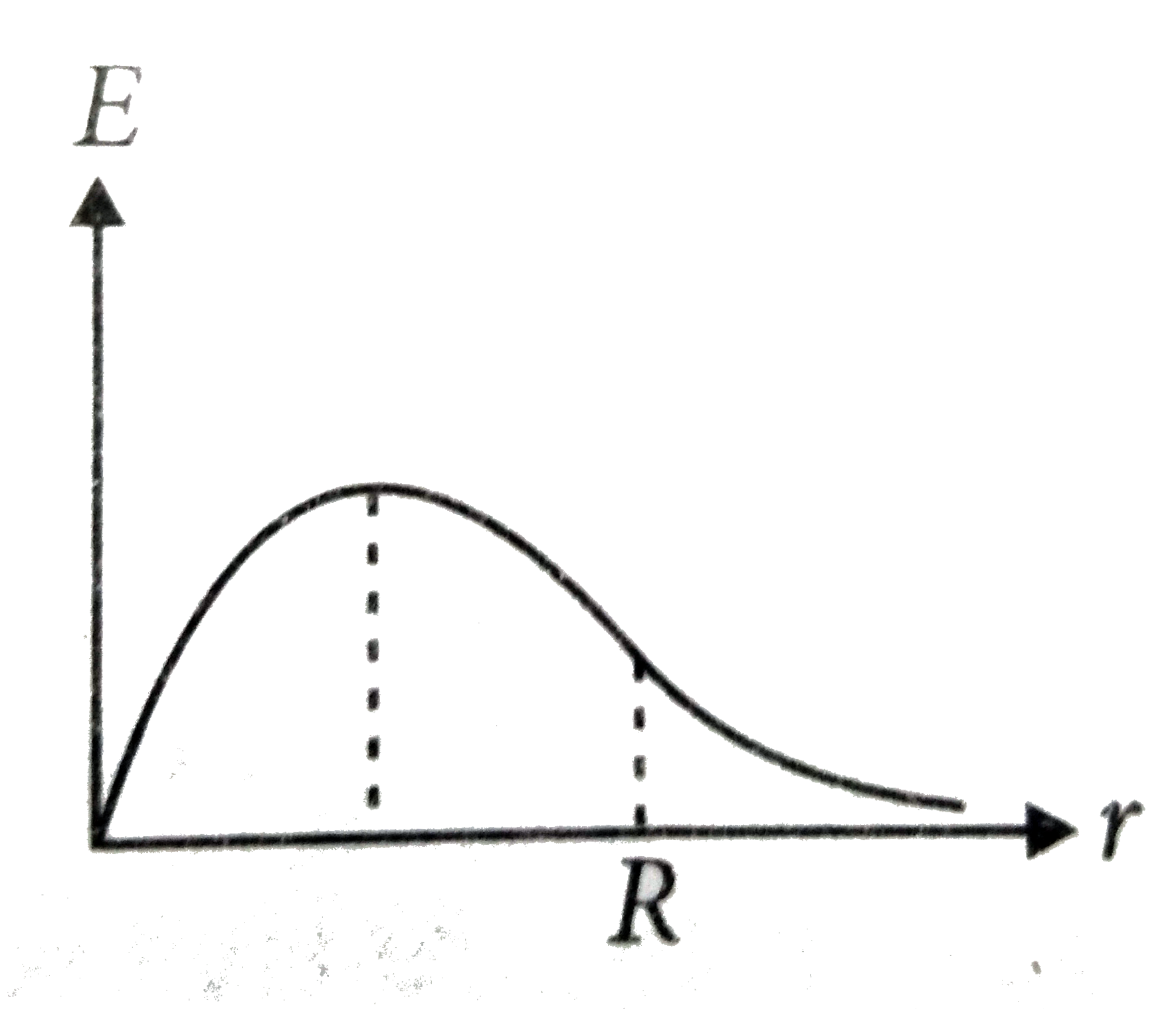
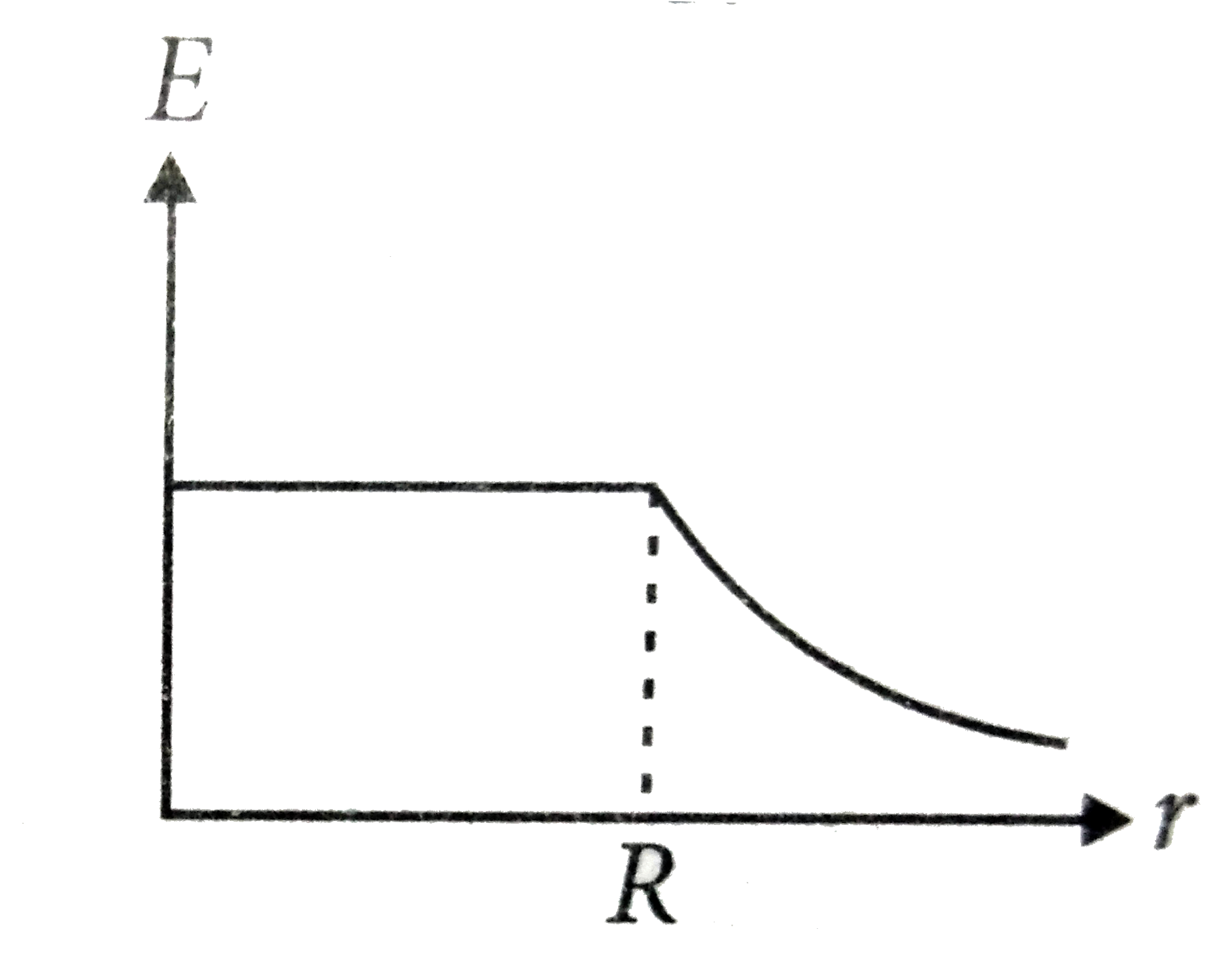
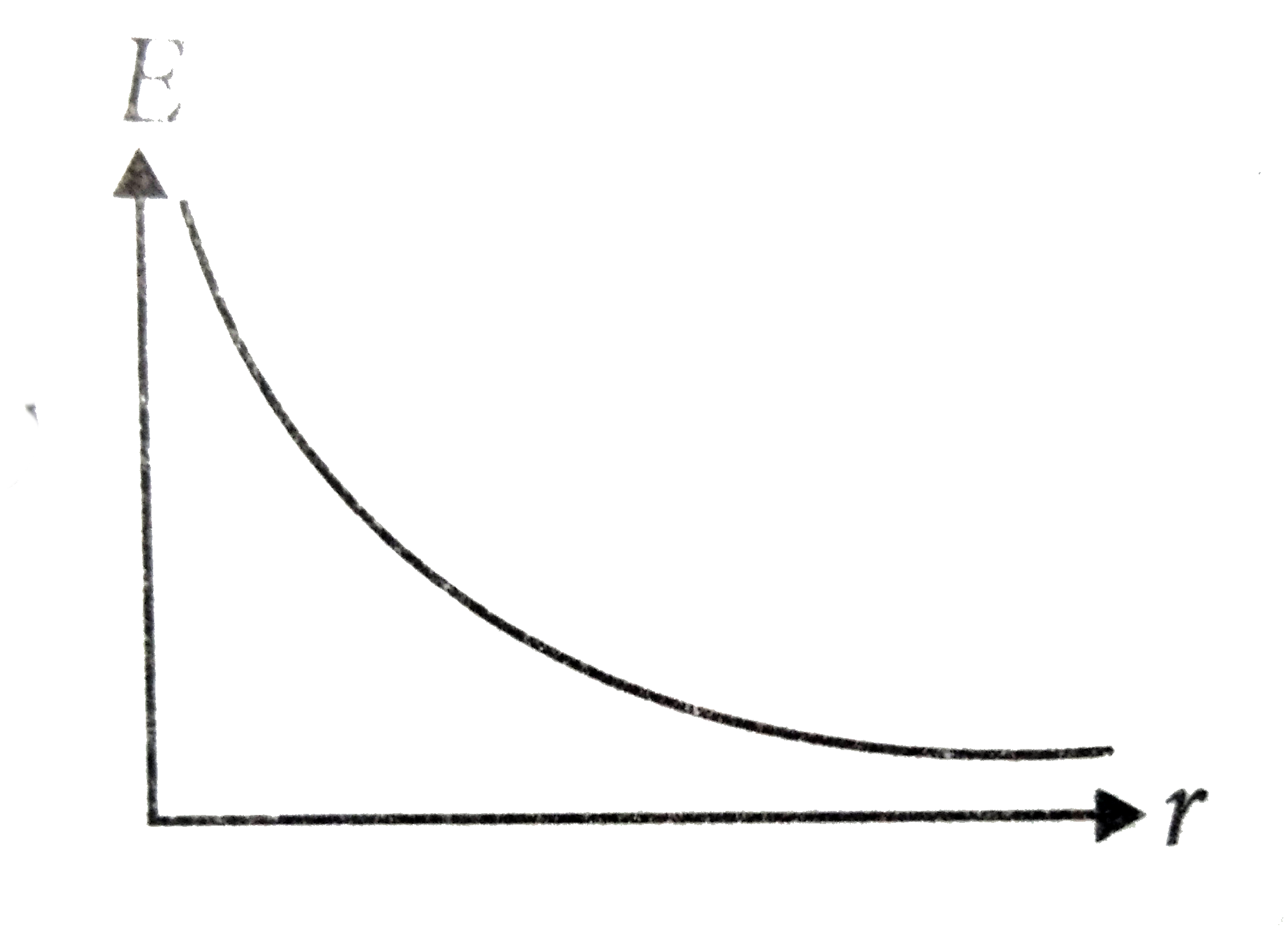
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
ELECTRIC CHARGES AND FIELDS
NCERT FINGERTIPS ENGLISH|Exercise Higher Order Thinking Skills|7 VideosELECTRIC CHARGES AND FIELDS
NCERT FINGERTIPS ENGLISH|Exercise NCERT Exemplar|5 VideosELECTRIC CHARGES AND FIELDS
NCERT FINGERTIPS ENGLISH|Exercise Application Of Gauss Law|9 VideosDUAL NATURE OF RADIATION AND MATTER
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 VideosELECTROMAGNETIC INDUCTION
NCERT FINGERTIPS ENGLISH|Exercise NCERT Exemplar|6 Videos
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS ENGLISH-ELECTRIC CHARGES AND FIELDS-HOTS
- Two point charges q(1)=-4muC and q(2)=8muC are lying on the y-axis. Th...
Text Solution
|
- Two spherical conductors B and C having equal radii and cayying equal ...
Text Solution
|
- A very long, straight, thin wire carries -3.60 nCm^(-1) of fixed negat...
Text Solution
|
- A system consits of a uniformly charged sphere of radius R and a surro...
Text Solution
|
- A charge is distributed with a linear density lamda over a rod of the ...
Text Solution
|
- When a charge of amount Q is given to an isolated metal plate X of sur...
Text Solution
|
- Let rho(r)=(Qr)/(piR^(4)) be the charge density distribution for a soi...
Text Solution
|
- A spherical insulator of radius R is charged uniformly with a charge Q...
Text Solution
|