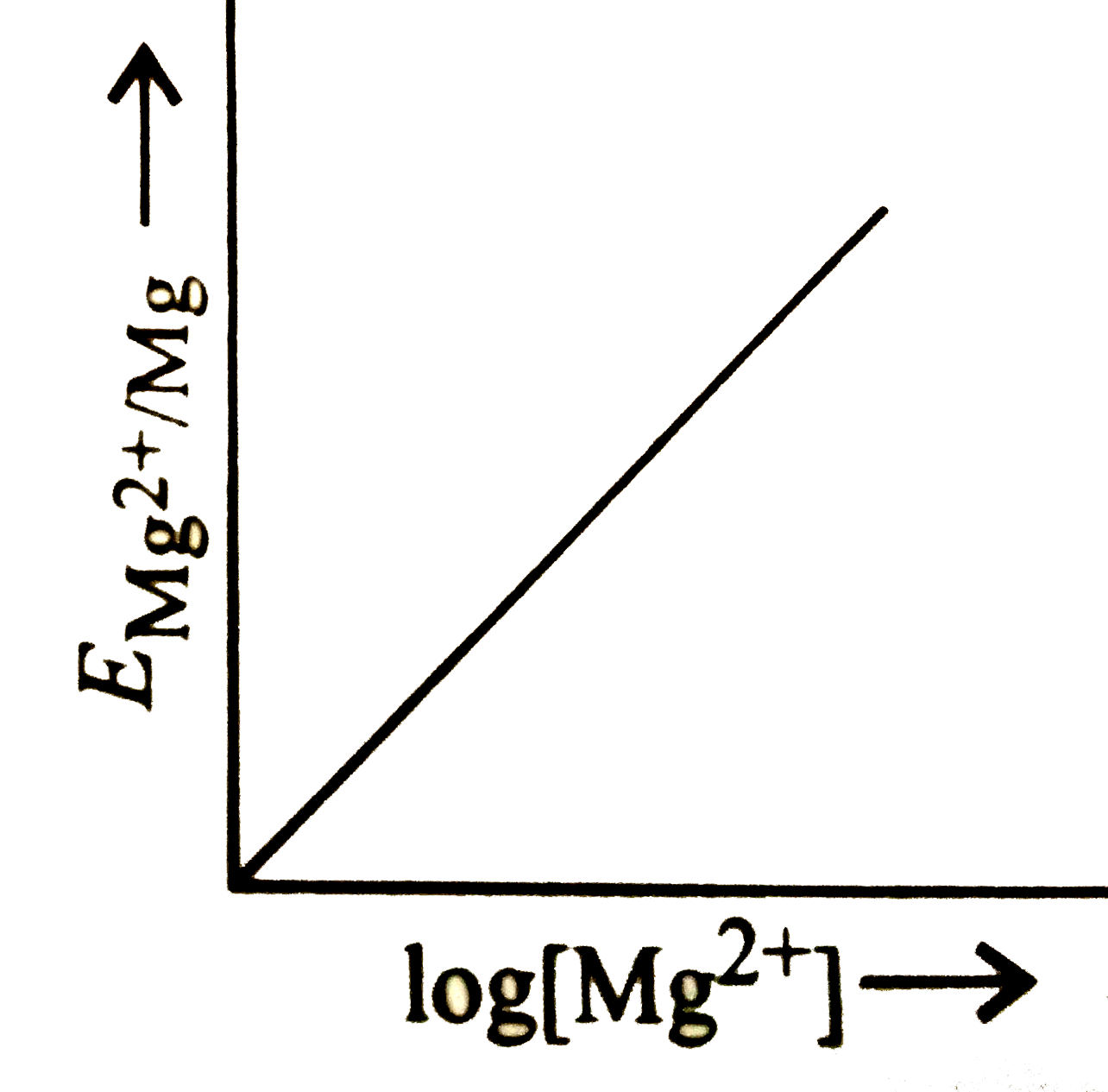
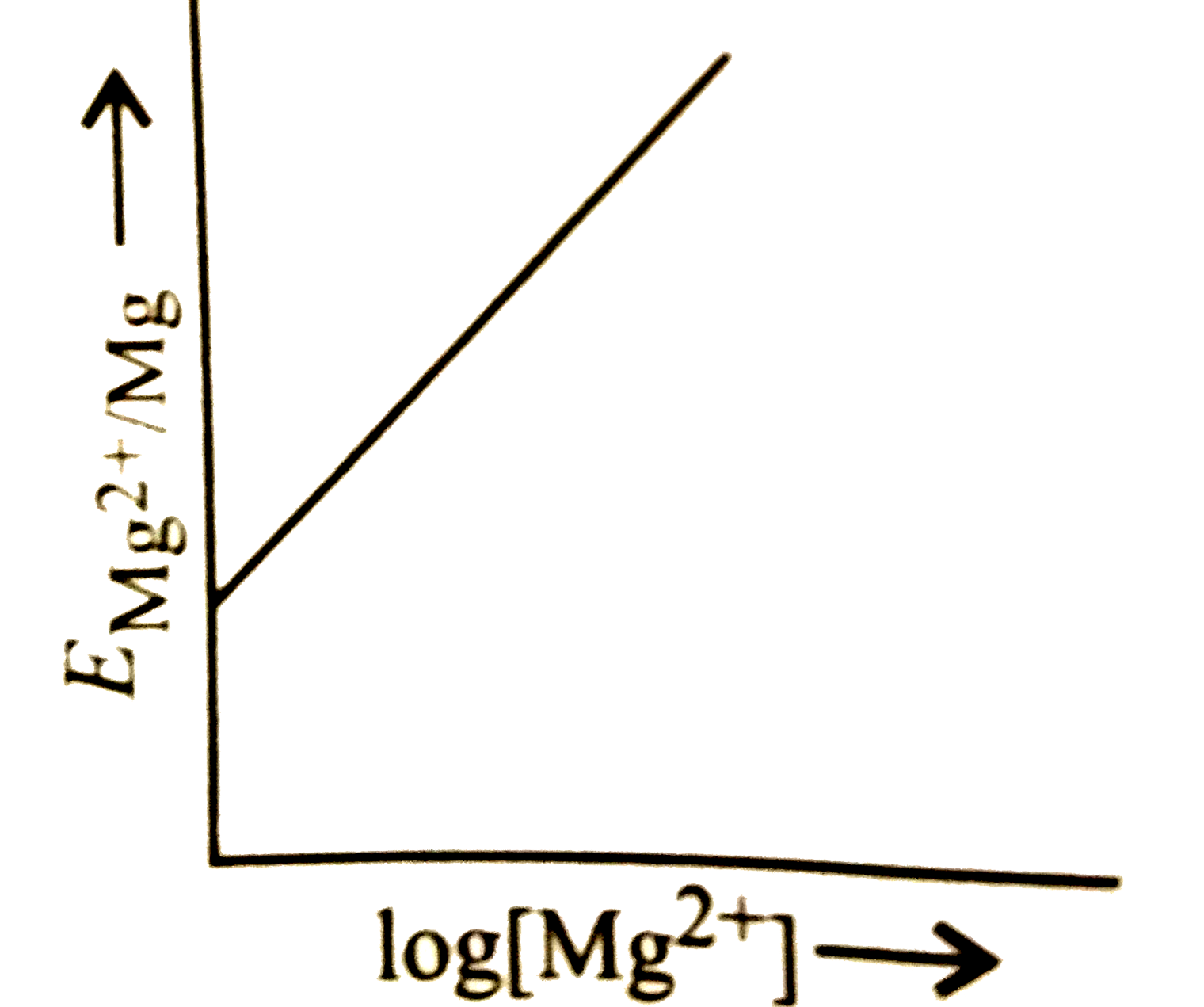
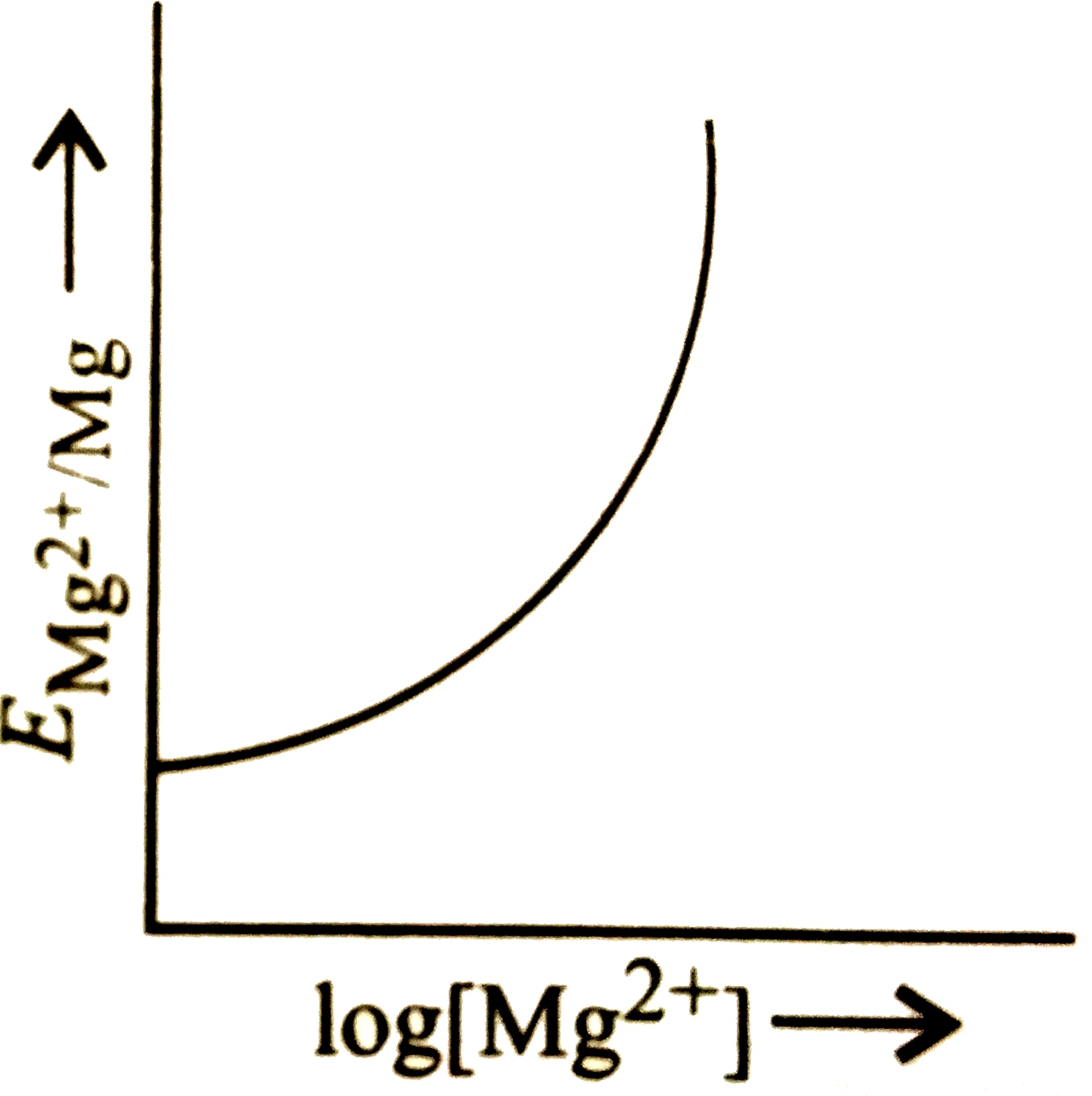
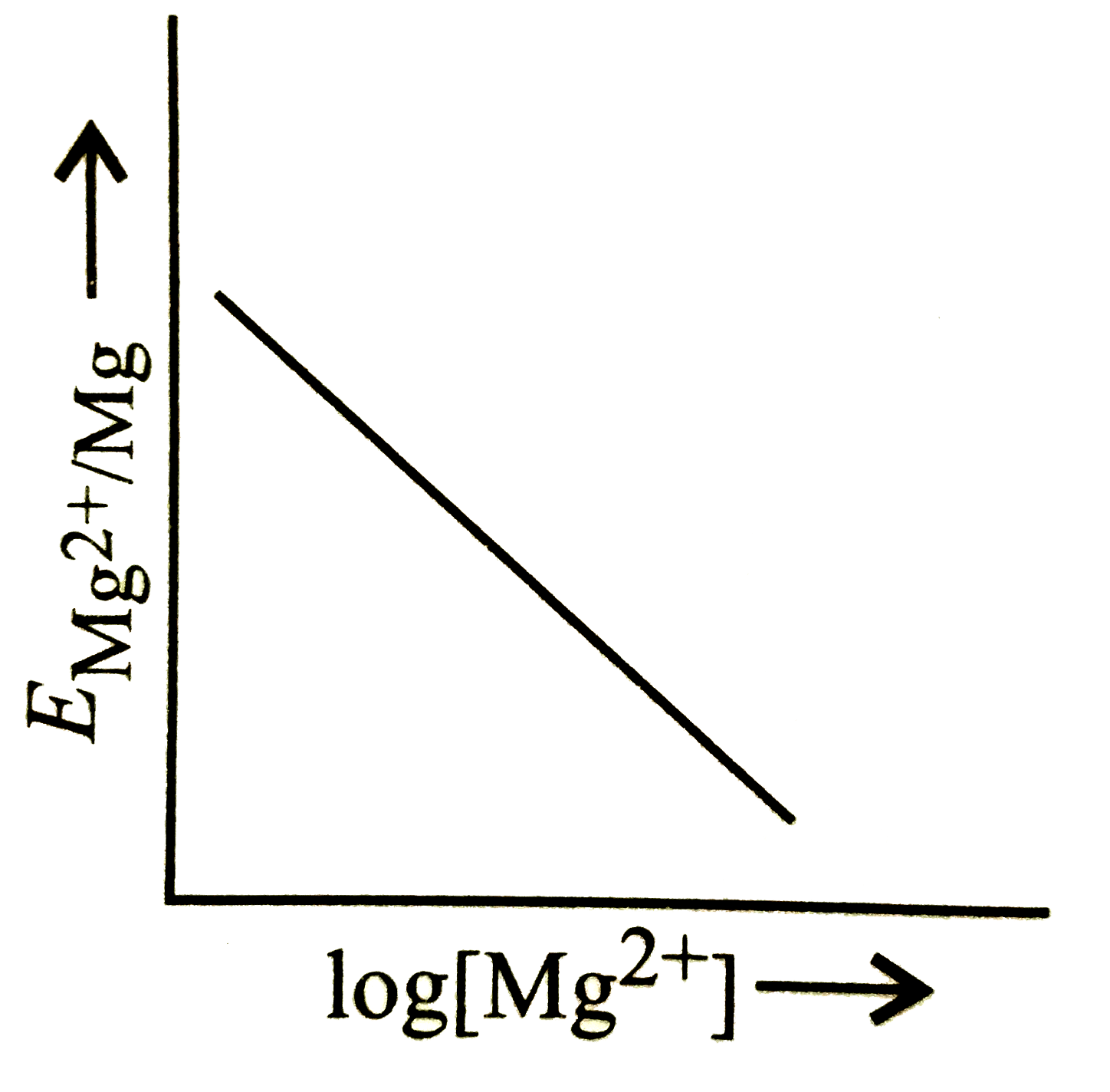
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
ELECTROCHEMISTRY
NCERT FINGERTIPS ENGLISH|Exercise ASSERTION & REASON|15 VideosELECTROCHEMISTRY
NCERT FINGERTIPS ENGLISH|Exercise Electrochemical Cell|1 VideosELECTROCHEMISTRY
NCERT FINGERTIPS ENGLISH|Exercise HOTS|10 VideosCOORDINATION COMPOUNDS
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 VideosGENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTS
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 Videos
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS ENGLISH-ELECTROCHEMISTRY-EXEMPLAR PROBLEMS
- Which cell will measure standard electrode potential of copper electro...
Text Solution
|
- Electrode potential for Mg electrode varies according to the equation ...
Text Solution
|
- Which of the following statement is correct?
Text Solution
|
- The difference between the electrode potentials of two electrons when ...
Text Solution
|
- Which of the following statement is not correct about an inert electro...
Text Solution
|
- An electrochemical cell an behave like an electrolytic cell when
Text Solution
|
- Which of the statements about solution of electrolytes is not correct?
Text Solution
|
- Using the data given below: E(Cr(2)O(7)^(2-)|Cr^(3+))^(@)=1.33V E(Cl...
Text Solution
|
- Using tha data given below is reducing potenial. E(Cr2O7^(2-)//Cr^(3...
Text Solution
|
- Using the data given below: E(Cr(2)O(7)^(2-)|Cr^(3+))^(@)=1.33V E(Cl...
Text Solution
|
- Using the data given below: E(Cr(2)O(7)^(2-)|Cr^(3+))^(@)=1.33V E(Cl...
Text Solution
|
- Using the data given below: E(Cr(2)O(7)^(2-)|Cr^(3+))^(@)=1.33V E(Cl...
Text Solution
|
- The quantity of charge required to obtain one mole of aluminium from A...
Text Solution
|
- The cell constant of a conductivity cell
Text Solution
|
- While charging the lead storage battery:
Text Solution
|
- Lambda((m)(NH(4)OH))^(@) is equal to
Text Solution
|
- In the electrolysis of aqueous sodium chloride solution which of the h...
Text Solution
|