Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
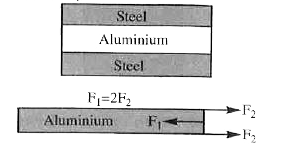
- Two steel rods and an aluminium rod of equal length l(0) and equal cro...
Text Solution
|
- Coefficient of linear expansion of brass and steel rods are alpha(1) a...
Text Solution
|
- Two rods, one of aluminium and other made of steel, having initial len...
Text Solution
|
- Two uniform metal rods one of aluminium of length l(1) and another mad...
Text Solution
|
- Two Aluminium rods and a steel rod of equal cross-sectional area and e...
Text Solution
|
- Three equal -length straight rods, of aluminium invar and steel all at...
Text Solution
|
- Two metal rods of lengths L(1) and L(2) and coefficients of linear exp...
Text Solution
|
- Two rods one of aluminium and the other made of steel having initial l...
Text Solution
|
- A meter scale calibarated for temperature T is used to measure the len...
Text Solution
|