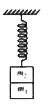
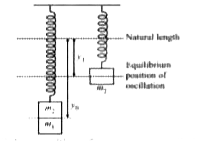
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
OSCILLATIONS AND WAVES
MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 1: SINGLE OPTION CORRECT TYPE (1 MARK))|16 VideosOSCILLATIONS AND WAVES
MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))|3 VideosOSCILLATIONS AND WAVES
MTG-WBJEE|Exercise WB JEE WORKOUT (CATEGORY 2: SINGLE OPTION CORRECT TYPE 2 MARKS)|15 VideosNUCLEAR PHYSIC
MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS|5 VideosPARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISM
MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS|15 Videos
Similar Questions
Explore conceptually related problems
MTG-WBJEE-OSCILLATIONS AND WAVES-WB JEE WORKOUT (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
- An object of mass m is performing simple harmonic motion on a smooth h...
Text Solution
|
- Two masses m(1) and m(2) are suspended w together by a light spring o...
Text Solution
|
- A whistle revolves in a circle with angular speed 0 = 20 rad/sec using...
Text Solution
|
- The equation of a transverse wave travelling along a spring is y = 4.0...
Text Solution
|
- Two blocks connected by a spring rest on a smooth ITIM horizontal pla...
Text Solution
|
- A block A of mass m connected with a spring of force constant k is exe...
Text Solution
|
- The ratio of the densities of oxygen and nitrogen is 16:14. At what te...
Text Solution
|
- An open pipe is in resonance in its 2nd harmonic with tuning fork of f...
Text Solution
|
- A simple pendulum of length 1 m with a bob of mass m swings with an an...
Text Solution
|
- A particle of mass m is located in a one dimensional potential field w...
Text Solution
|