Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
U-LIKE SERIES-CBSE EXAMINATION PAPER 2020 -SECTION D
- Use Gauss's law to show that due to uniformly charged spherical shell ...
Text Solution
|
- Two point charges of +1muC and +4muC are kept 30 cm apart. How far fro...
Text Solution
|
- Two point charges q(1) and q(2) are kept r distance apart in a uniform...
Text Solution
|
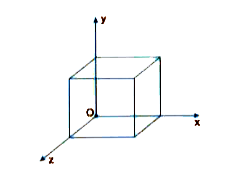
- A cube of side 20 cm is kept in a region as shown in the figure. An el...
Text Solution
|
- A circular loop of radius R carries a current I. Obtain an expression ...
Text Solution
|
- A conducting rod of length 2 m is placed on a horizontal table in nort...
Text Solution
|
- Obtain the expression for the deflecting torque acting on the current ...
Text Solution
|
- Particles of mass 1.6xx10^(-27) kg and charge 1.6xx10^(-19)C are accel...
Text Solution
|
- Derive lens maker's formula for a biconvex lens.
Text Solution
|
- A point object is placed at a distance of 12 cm on the principal axis ...
Text Solution
|
- What is a wavefront? How does it propagate? Using Huygens' principle, ...
Text Solution
|
- A parallel beam of light of wavelength 500 nm falls on a narrow slit a...
Text Solution
|