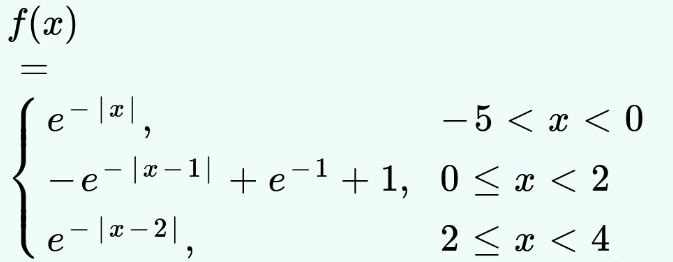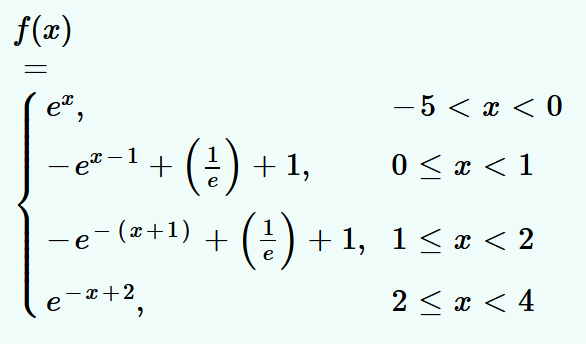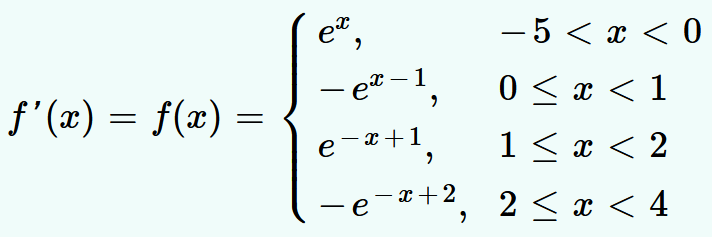लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
ALLEN HINDI-DIFFERENTIABILITY-Exercise-5 [B]
- यदि f(x)= {(e^(-|x|)",",-5 lt x lt 0),(-e^(-|x-1|) + e^(-1) + 1",",0le...
Text Solution
|
- यदि f:RtoR एक फलन जो f(x)="max"(x,x^(3)) द्वारा परिभाषित है तब उन बिंद...
Text Solution
|
- f(x)= [x] sin (pi x), x = k (k एक पूर्णांक है) पर इसके बाये अवकलज का म...
Text Solution
|
- निम्न में से कौनसा फलन x=0 पर अवकलनीय है-
Text Solution
|
- यदि R वास्तविक संख्याओं का समुच्चय है, तो सिद्ध कीजिए कि, f:R rarr...
Text Solution
|
- फलन f(x) ={(tan^(-1)x ,"यदि ",|x| le 1),((1)/(2) |x|-1,"यदि ","if " |x...
Text Solution
|
- फलन f: R rarr R इस प्रकार है कि f(1)= 3 तथा f'(1)= 6, तो underset(x ra...
Text Solution
|
- माना f : R to R तथा g, R to R f(x) = {:{( x+a , x lt0),( |x-1...
Text Solution
|
- माना एक विषम फलन f: [-2a, 2a] rarr R इस प्रकार है की x in [a, 2a] के ल...
Text Solution
|
- दिया गया फलन y= ||x|-1|. जिन बिन्दुओ को छोड़कर सभी वास्तविक संख्याओं के...
Text Solution
|
- सभी x(1),x(2)inR के लिए यदि |f(x(1))-f(x(2))|lt(x(1)-x(2))^(2) है। बिं...
Text Solution
|
- यदि f(x)= न्यूनतम (1, x^(2), x^(3)) , तो-
Text Solution
|
- माना g(x)= ((x-1)^(n))/(ln cos^(m) (x-1)), 0 lt x lt 2,m व n पूर्णांक ...
Text Solution
|
- माना लीजिये f: R rarr R एक फलन है, जो समीकरण f(x+y) = f(x) + f(y), A...
Text Solution
|
- यदि f(x)= {(-x-(pi)/(2)",",x le -(pi)/(2)),(-cos x,-(pi)/(2) lt x le 0...
Text Solution
|
- दिया है, f(x) = {{:(x^(2)|"cos"(pi)/(x)|,x ne 0),(0,x = 0):}, x in R, ...
Text Solution
|