Text Solution
Verified by Experts
Topper's Solved these Questions
[II PUC PHYSICS] ANNUAL EXAM QUESTION PAPER MARCH-2016
SUNSTAR PUBLICATION|Exercise PART-D ( Answer any two of the following questions)|3 Videos[II PUC PHYSICS] ANNUAL EXAM QUESTION PAPER MARCH-2016
SUNSTAR PUBLICATION|Exercise PART-D (Answer any two of the following).|3 Videos[II PUC PHYSICS] ANNUAL EXAM QUESTION PAPER MARCH-2016
SUNSTAR PUBLICATION|Exercise PART-B (Answer any five of the following questions.)|8 VideosSUPPLEMENTARY EXAM QUESTION PAPER JUNE-2019
SUNSTAR PUBLICATION|Exercise Part-C|18 Videos
Similar Questions
Explore conceptually related problems
SUNSTAR PUBLICATION-[II PUC PHYSICS] ANNUAL EXAM QUESTION PAPER MARCH-2016-PART-C ( Answer any five of the following questions)
- What is a transformer ? Mention two sources of energy loss in a transf...
Text Solution
|
- What are the characteristics of nuclear forces?
Text Solution
|
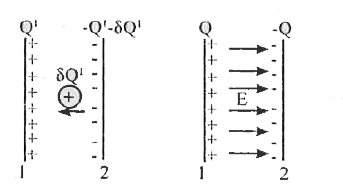
- Derive the expression for energy stored in a charged capacitor.
Text Solution
|
- What is an amplifier? Draw the simple circuit of transistor amplifier ...
Text Solution
|
- Mention the types of transmission media.
Text Solution
|
- Arrive at an expression for drift velocity.
Text Solution
|
- Describe the coil and barmagnet experiment to demonstrate the phenomen...
Text Solution
|
- Write any five properites of ferromagnetic materials
Text Solution
|