Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
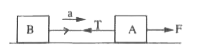
- Two identical blocks A and B each of mass M are connected to each othe...
Text Solution
|
- Figure shows two identical blocks each of mass m kept on a smooth floo...
Text Solution
|
- In the system shown in the figure, all surfaces are smooth. Block A an...
Text Solution
|
- Two blocks of masses 10 kg and 20 kg are connected by a massless strin...
Text Solution
|
- समान द्रव्यमान m के दो गुटके एक-दूसरे से भारहीन डोरी की सहायता से बाँध...
Text Solution
|
- Two blocks of masses m and M are connected by an inextensible light st...
Text Solution
|
- Four blocks each of mass M connected by a massless strings are pulled ...
Text Solution
|
- Two identical blocks A and B each of mass M are connected to each othe...
Text Solution
|
- Two identical blocks A and B each of mass M are connected to each othe...
Text Solution
|