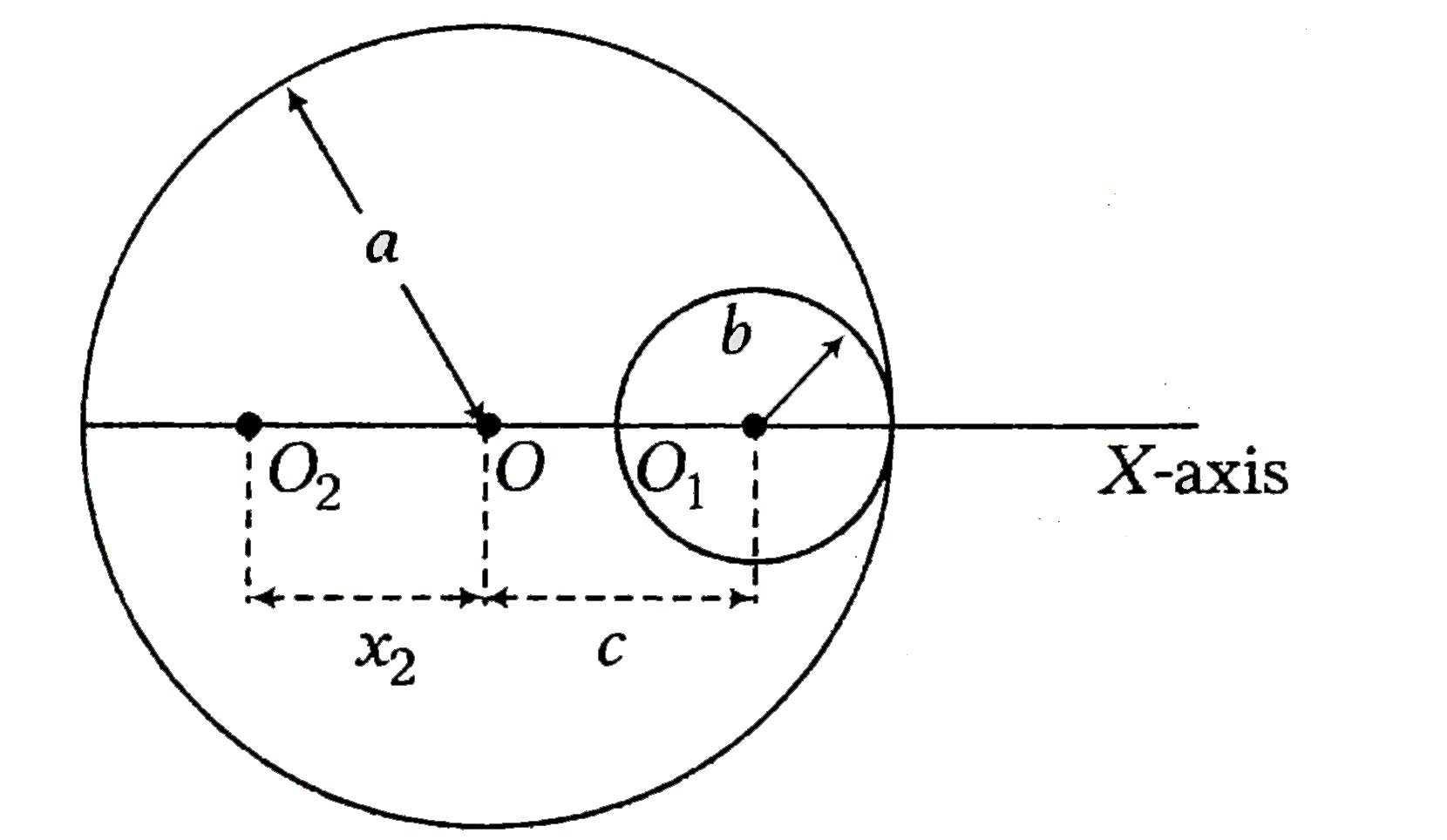
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform circular disc of radius a is taken. A circular portion of ra...
Text Solution
|
- A circular disc of radius R is removed from a bigger circular disc of ...
Text Solution
|
- A small disc of radius 2cm is cut from a disc of radius 6cm. If the di...
Text Solution
|
- A uniform circular disc of radius a is taken. A circular portion of ra...
Text Solution
|
- From a circular disc of radius R, a square is cut out with a radius as...
Text Solution
|
- 2R त्रिज्या की एक बड़ी चकती में से R त्रिज्या की एक वृत्तीय चकती इस प्र...
Text Solution
|
- From a uniform disc of radius R, a small disc of radius (R)/(2) is cut...
Text Solution
|
- Find the mass center of the uniform disk of radius 'a' from wh...
Text Solution
|
- The diameter of a circular disk of uniform thickness is 56 cm. | As sh...
Text Solution
|