Home
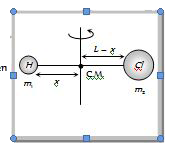
Class 11
PHYSICS
The moment of inertia of HCl molecule ab...

The moment of inertia of `HCl` molecule about an axis passing through its centre of mass and perpendicular to the line joining the `H^+` and `Cl^-` ions will be (if the inter atomic distance is `1A^@`)

A

`0.61xx10^(-47)kg.m^(2)`

B

`1.61xx10^(-47)kg.m^(2)`

C

`0.061xx10^(-47)kg.m^(2)`

D

0

Text Solution

Verified by Experts

The correct Answer is:
B
If `r_(1)` and `r_(2)` are the respective distances of particles `m_(1)` and `m_(2)` from the centre of mass then
`m_(1)r_(1)=m_(2)r_(2)implies1xx x=35.5xx(L-x)impliesx=35.5(1-x)`
`impliesx=0.973ÅandL-x=0.027Å`
Moment of inertia of the system about centre of mass `I=m_(1)x^(2)+m_(2)(L-x)^(2)`
`I=1"amu"xx(0.973Å)^(2)+35.5"amu"xx(0.027Å)^(2)`
Substituting 1 a.m.u. = `1.67xx10^(-27)kg and 1Å=10^(-10)m`
`l=1.62xx10^(-47)kgm^(2)`
Promotional Banner

Topper's Solved these Questions

  • ROTATIONAL MOTION

    ERRORLESS |Exercise Practice Problems (Problems based on centre of mass)|12 Videos

  • ROTATIONAL MOTION

    ERRORLESS |Exercise Practice Problems (Problems based on angular displacement, velocity and acceleration)|16 Videos

  • NEWTONS LAWS OF MOTION

    ERRORLESS |Exercise Self Evaluation Test|16 Videos

  • SIMPLE HARMONIC MOTION

    ERRORLESS |Exercise simple Harmonic Motion|21 Videos

Similar Questions

Explore conceptually related problems

The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane

Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is

The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is

Two partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in kg-m^(2))

Calculate the moment of inertia of an oxygen molecule about an axis passing through its centre of mass and perpendicular to the internuclear axis. Take Mass of O-atom =2.67xx10^(-26)kg Interatiomic distance =1.2xx10^(-10)m

Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.

Find the moment fo inertia of the hydrogen molecules about an axis passing through its centre of mass and perpendicular to the internuclear axis. Given mass of H-atom = 1.7 xx 10^(-27) kg , interatomic distance = 4xx 10^(-10)m