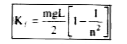Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform chain of length 'L' and mass 'm' is on a smooth horizontal t...
Text Solution
|
- A uniform chain of length l and mass m overhangs a smooth table with i...
Text Solution
|
- A chain of uniform mass m and length L is held on a frictionless table...
Text Solution
|
- A uniform chain of length 1 and mass m is kept on a smooth table. It i...
Text Solution
|
- একটি মসৃন অনুভূমিক টেবিলের উপর একটি শিকল রাখা আছে। শিকলের দৈর্ঘ্যের 1/...
Text Solution
|
- A uniform chain of mass m and length l is on a smooth horizontal table...
Text Solution
|
- A uniform chain of length l is lying on a rough table and (1)/(n) th o...
Text Solution
|
- A chain is on a smooth horizontal table with 1/3 of its length hanging...
Text Solution
|
- A chain of mass m and length l is kept on a horizontal frictionless ta...
Text Solution
|