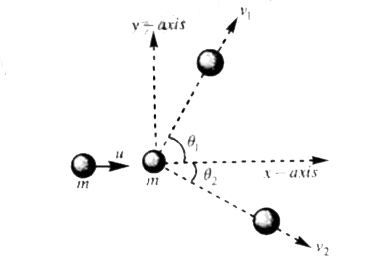
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Prove that in case of oblique elastic collision of two particles of eq...
Text Solution
|
- A particle A suffers an oblique elastic collision particle B that is a...
Text Solution
|
- In a perfectly elastic collision in two dimensions between two particl...
Text Solution
|
- Show that two equal masses undergo oblique elastic collision will move...
Text Solution
|
- If a particle elastically collides obliquely with a particle of same m...
Text Solution
|
- If a particle elastically collides obliquely with a particle of same m...
Text Solution
|
- Prove that in case of oblique elastic collision of two particles of eq...
Text Solution
|
- Two bodies of equal masses moving mutually at right angles to each oth...
Text Solution
|
- Prove that in case of oblique elastic collision of two particles of eq...
Text Solution
|