Home
Class 12
PHYSICS
A heating element of resistance r is fit...

A heating element of resistance r is fitted inside an adiabatic cylinder which carries a frictionless piston of mass in and cross-section A as shown in diagram. The cylinder contains one mole of an ideal diatomic gas. The current flows through the element such that the temperature rises with time `t` as `DeltaT = alphat + 1/2beta t^2` (`alpha` and `beta` are constants), while pressure remains constant. The atmospheric pressure above the piston is `P_0`. Then

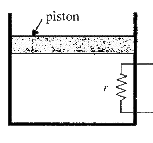
the rate of increase in internal energy is `5/2 R (alpha + beta t)`
the current flowing in the element is `sqrt(5/(2r)(alpha +betat))`
the piston moves upwards with constant acceleration 
the piston moves upwards with constant speed

Promotional Banner

Topper's Solved these Questions

  • QUESTION PAPER 2014

    WB JEE PREVIOUS YEAR PAPER|Exercise PHYSICS (CATEGORY II)|10 Videos

  • QUESTION PAPER 2013

    WB JEE PREVIOUS YEAR PAPER|Exercise Category-III|5 Videos

  • QUESTION PAPER 2015

    WB JEE PREVIOUS YEAR PAPER|Exercise PHYSICS (CATEGORY III)|5 Videos

Similar Questions

Explore conceptually related problems

The plot V alpha T at constant pressure

For an adiabatic process of an ideal monatomic gas the pressure and the temperature are related as p prop T^(C ) . Find out the value of C.

70 cal of heat is required to raise the temperature of 20 moles of an ideal diatomic gas at constant pressure from 30^@C . The amount of heat required (in cal) to raise the temperature of the same gas through the same range ( 30^@C to 35^@C ) at constant volume is

One mole of an ideal monoatomic gas is heated at constant pressure from 0^@C to 100^@C . Calculate work done.

For an adiabatic process of an ideal monatomic gas, the pressure and temperature are related as P prop T^c . Find out the value of C.

Temperature of an ideal gas is 340 K. At constant pressure the gas is so heated volume increases by 18% . What is the final temperature of the gas ?

For a fixed mass of a gas at constant volume, pressure rises when temperature increases,and vice versa Explain from the kinetic theory.

An ideal mono-atomic gas of given mass is heated at constant pressure. In this process, the fraction of supplied heat energy used for the increase of the internal energy of the gas is