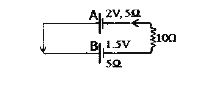Home
Class 12
PHYSICS
Two cells A and B ofe.m.f. 2V and 1.5V r...

Two cells A and B ofe.m.f. 2V and 1.5V respectively, are connected as shown in figure through an external resistance 10 ohm. The internal resistance of each cell is 5 ohm. The potential difference `E_(A) and E_(B)` across the terminals of the cells A and B respectively are

A

`E_(A) = 2.0V, E_(a) = 1.5 V`

B

`E_(A) = 2.125V, E_(g) = 1.375V`

C

`E_(A) = 1.875V, E_(g) = .625 V`

D

`E_(A) = 1.875V, E_(g) = 1.375V`

Text Solution

Verified by Experts

Promotional Banner

Topper's Solved these Questions

  • QUESTION PAPER 2015

    WB JEE PREVIOUS YEAR PAPER|Exercise PHYSICS (CATEGORY III)|5 Videos

  • QUESTION PAPER 2015

    WB JEE PREVIOUS YEAR PAPER|Exercise PHYSICS (CATEGORY III)|5 Videos

  • QUESTION PAPER 2014

    WB JEE PREVIOUS YEAR PAPER|Exercise PHYSICS (CATEGORY III)|3 Videos

  • QUESTION PAPER 2016

    WB JEE PREVIOUS YEAR PAPER|Exercise PHYSICS|40 Videos

Similar Questions

Explore conceptually related problems

The internal resistance of a cell of emf E is r, and external resistance is R. What is the potential about the external Resistance

When a resistance of 12 Omega is connected with a cell of emf 1.5 V, 0.1A current flows through the resistance. Internal resistance of the cell is—

When a resistance of 12 Omega is conencted with a cell of emf 1.5 V,0.1 A current flows through the resistance internal resistance of the cell is

Two identical cells each of emf E and internal resistance r are connected in parallel with an external resistance R. To get maximum power developed across R, the value of R is

Two cells each of emf e but internal resistances r_1 and r_2 are connected in series through an external resistance R. IF the potential difference across the first cell is zero while current flows,the relation of R in terms of r_1 and r_2 is

Two cells each of emf e but internal resistance r_1 and r_2 are connected in series through an external resistance R. IF the potential difference across the first cell is szero while current flow, the relation of R in terms of r_1 and r_2