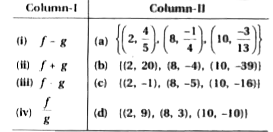Home
Class 11
MATHS
Let f= {(2,4), (5,6), (8, -1), (10, -3) ...

Let `f= {(2,4), (5,6), (8, -1), (10, -3) and g{(2, 5) (7, 1), (8, 4), (10, 13), (11,5)}` be two real functions. Then, match the following.

The domain of `f-g, f+ g, f.g, (f)/(g)` is domain of `f nn` domain of g. Then, find their images.

Text Solution

Verified by Experts

The correct Answer is:
`(i) rarr (c ), (ii) rarr (d), (iii) rarr (b), (iv) rarr (a)`
Promotional Banner

Topper's Solved these Questions

  • RELATIONS AND FUNCTIONS

    KUMAR PRAKASHAN|Exercise Solutions of NCERT Exemplar Problems (True/False)|5 Videos

  • RELATIONS AND FUNCTIONS

    KUMAR PRAKASHAN|Exercise Solutions of NCERT Exemplar Problems (Question of Module)|16 Videos

  • RELATIONS AND FUNCTIONS

    KUMAR PRAKASHAN|Exercise Solutions of NCERT Exemplar Problems (Objective Type Questions)|12 Videos

  • PROBABILITY

    KUMAR PRAKASHAN|Exercise PRACTICE WORK|40 Videos

  • SEQUENCE AND SERIES

    KUMAR PRAKASHAN|Exercise Solutions of NCERT Exemplar Problems -Question of Module|19 Videos

Similar Questions

Explore conceptually related problems

If the mapping f and g are given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)} , write down pairs in the mapping fog and gof .

If f(x)= sqrtx and g(x)= x be two functions defined in the domain R^(+) uu {0} , then find the value of (f+g) (x) .

f(x) is a real valued function f(x) = (1)/(sqrt(5x-3)) . Find the domain of f(x).

Let f and g be two real functions given by f= {(0, 1), (2,), (3, -4), (4, 2), (5, 1)} and g= {(1,0), (2,2), (3,-1), (4,4),(5,3)} . Find Domain.

If f and g are two real valued functions defined as f(x)= 2x+1 and g(x)= x^(2)+1 , then find (f)/(g) .

Let f: {2, 3, 4, 5} rarr {3, 4, 5, 9} and g : {3, 4, 5, 9} rarr {7, 11, 15} be functions defined as f (2) = 3, f(3) = 4, f(4) = f(5) = 5 and g(3) = g(4) = 7 and g(5) = g(9) = 11. Find gof.

Let f(x)=x^(2) and g(x)=2x+1 be two real functions. Find (f+g) (x), (f-g) (x), (fg) (x), (f/g) (x) .

If f and g are two real valued functions defined as f(x)= 2x+1 and g(x)= x^(2)+1 , then find f+g

If f and g are two real valued functions defined as f(x)= 2x+1 and g(x)= x^(2)+1 , then find f-g

Let f , g and h be functions from R to R . Show that , (f +g) oh = foh + goh (f.g) oh = (foh)+ (goh)