Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MBD-ARITHMETIC PROGRESSION-EXERCISE
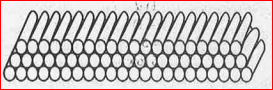
- 200 logs are stacked in the following manner : 20 logs in the bottom r...
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- If it is an arithmetic progressions, find out the common difference. :...
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find out which of the following sequences are arithmetic progressions....
Text Solution
|
- Find the common difference of the AP and write the next two terms :- 5...
Text Solution
|
- Find the common difference of the AP and write the next two terms :- 7...
Text Solution
|
- Find the common difference of the AP and write the next two terms :- 0...
Text Solution
|
- Find the common difference of the AP and write the next two terms :- 1...
Text Solution
|
- The n^(th) term of a sequence is given by Tn = 2n + 7. Show that it i...
Text Solution
|
- Show that the sequence defined by Tn = 4n + 7 is an A.P. Also, find it...
Text Solution
|
- Show that the sequence whose n^(th) term is 2n^2 + n + 1 is not an A....
Text Solution
|
- Find out which of the following sequences are A.P. for those which are...
Text Solution
|
- Find out which of the following sequences are A.P. for those which are...
Text Solution
|
- Find out which of the following sequences are A.P. for those which are...
Text Solution
|