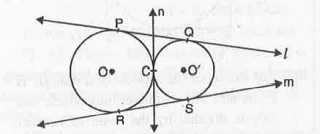
In the figure, two circles touch each other externally at C. Prove that the common tangent at C bisects the other two common tangents.

Two circles of radii 4cm and 1cm touch each other externally and theta is the angle contained by their direct common tangents. Find sin θ.

Two circles with radii a and b touch each other externally such that theta is the angle between the direct common tangents, (a > bgeq2) . Then prove that theta=2sin^(-1)((a-b)/(a+b)) .

The centres of two circles C_(1) and C_(2) each of unit radius are at a distance of 6 unit from each other. Let P be the mid-point of the line segment joining the centres of C_(1) and C_(2) and C be a circle touching circles C_(1) and C_(2) externally. If a common tangent to C_(1) and C passing through P is also a common tangent to C_(2) and C, then the radius of the circle C, is

Three circles touch one another externally. The tangents at their points of contact meet at a point whose distance from a point of contact is 4. Find the ratio of the product of the radii to the sum of the radii of the circles.

If two straight lines intersect each other, then prove that the ray opposite to the bisector of one of the angles so formed bisects the vertically opposite angles.

Two circles, each of radius 5 units, touch each other at (1, 2). If the equation of their common tangent is 4x + 3y = 10, find the equations of the circles.

Two circles touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ = TR

If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.

In fig., two circles with centres O, O' touch externally at a point A. A line through A is drawn to intersect these circles in B and C. Prove that the tangents at B and C are parallel.

Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.