Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
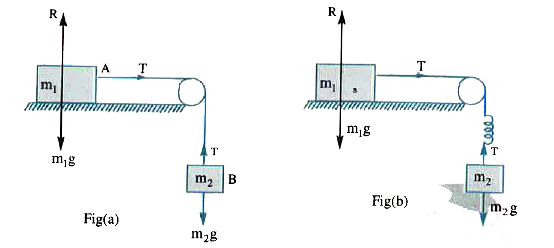
- A block A of mass 8 kg is placed on a frictionless horizontal table . ...
Text Solution
|
- A light string passes over a frictionless pulley. To one of its ends a...
Text Solution
|
- A block A of mass 7 kg is placed on a frictionless table. A thread tie...
Text Solution
|
- 8 kg तथा 12 kg के दो पिण्डो को किसी हल्की अवितान्य डोरी, जो घर्षणरहित ...
Text Solution
|
- 8 किग्रा तथा 12 किग्रा के दो पिण्डो को किसी हल्की अवितान्य डोरी, घर्ष...
Text Solution
|
- द्रव्यमान 10 किग्रा का एक ब्लॉक एक क्षैतिज मेज पर रखा है जिससे एक डोरी...
Text Solution
|
- द्रव्यमान 3.0 किग्रा का एक पिण्ड एक घर्षण रहित क्षैतिज मेज पर रखा है ज...
Text Solution
|
- Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless ...
Text Solution
|
- A block A of mass 8 kg is placed on a frictionless horizontal table. A...
Text Solution
|