Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
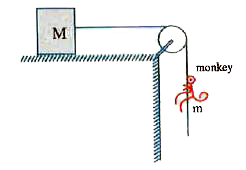
- A monkey of mass m clings to a rope over a fixed pulley . The opposi...
Text Solution
|
- The ballon the light rope and the monkey shown in figure are at rest ...
Text Solution
|
- A monkey of mass m clings a rope to a slung over a fixed pulley .The o...
Text Solution
|
- A monkey of mass m clings a rope to a slung over a fixed pulley .The o...
Text Solution
|
- A monkey of mass 'm' climbs up to a rope hung over a fixed pulley with...
Text Solution
|
- A monkey of mass m climbs up to a rope hung over a fixed pulley. The o...
Text Solution
|
- A cat of mass m = 1 kg climbs to a rope hung over a leight frictionles...
Text Solution
|
- A balloon of mass M with a light rope having monkey on the rope is in ...
Text Solution
|
- A monkey of mass m clings to a rope over a fixed pulley. The opposite ...
Text Solution
|