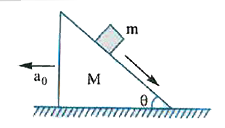
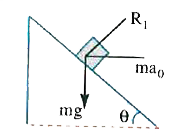
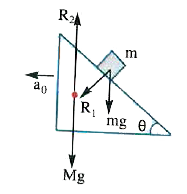
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A prism of mass M is placed on a horizontal surface . A block of mass ...
Text Solution
|
- All the surfaces shownin figure are assumed to be frictionless. The bl...
Text Solution
|
- A block of mas m is placed on a triangular block of mas m, which in tu...
Text Solution
|
- A block of mass m is placed on the block of mass M as shown in figure....
Text Solution
|
- A block of mass 10 kg is sliding on a surface inclined at 30^(@) with ...
Text Solution
|
- Prism 1 of mass m1 and width angle alpha (see figure) rests on a horiz...
Text Solution
|
- Assuming all the surfaces to be smooth, find the acceleration of the t...
Text Solution
|
- A heavy mass m slides down a triangular prism of mass M . The prism li...
Text Solution
|
- चित्र 11.W2 में एक घर्षणरहित क्षैतिज सतह पर त्रिभुजाकार ब्लॉक रखा हुआ ...
Text Solution
|