Home
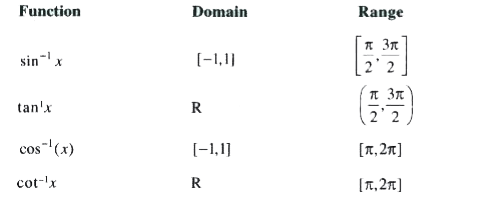
Class 11
MATHS
While defining inverse trigonometric fun...

While defining inverse trigonometric functions, a new system is followed where domains and ranges have been redefined as follows:

`sin^(-1)(-x)` is equal to

A

`-sin^(-1)x`

B

`pi+sin^(-1)x`

C

`2pi-sin^(-1)x`

D

`3pi-cos^(-1)sqrt(1-x^(2)),xgt0`

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • INVERSET TRIGONOMETRIC FUNCTIONS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) STATEMENT TYPE QUESTIOS)|2 Videos

  • INVERSET TRIGONOMETRIC FUNCTIONS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIOS)|1 Videos

  • INVERSET TRIGONOMETRIC FUNCTIONS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (LEVEL-II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)|6 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    AAKASH SERIES|Exercise PRACTICE EXERCISE|37 Videos

  • LIMITS

    AAKASH SERIES|Exercise PRACTICE EXERCISE|143 Videos

Similar Questions

Explore conceptually related problems

Find the domain and the range of the real function f defined by f(x)=sqrt((x-1))

The domain of the function f defined by f(x)= sqrt(4-x) + (1)/(sqrt(x^(2)-1)) is equal to

Find the domain and the range of the real function f defined by f(x)=|x-1|

Find the domain and range of the function f(x) = (x)/(1+x^2) .

Find the domain and range of the function f(x) = |x|+|1+x|

Find the domain and range of the function: f(x) = ([x]+[-x]+1)/(x-[x])