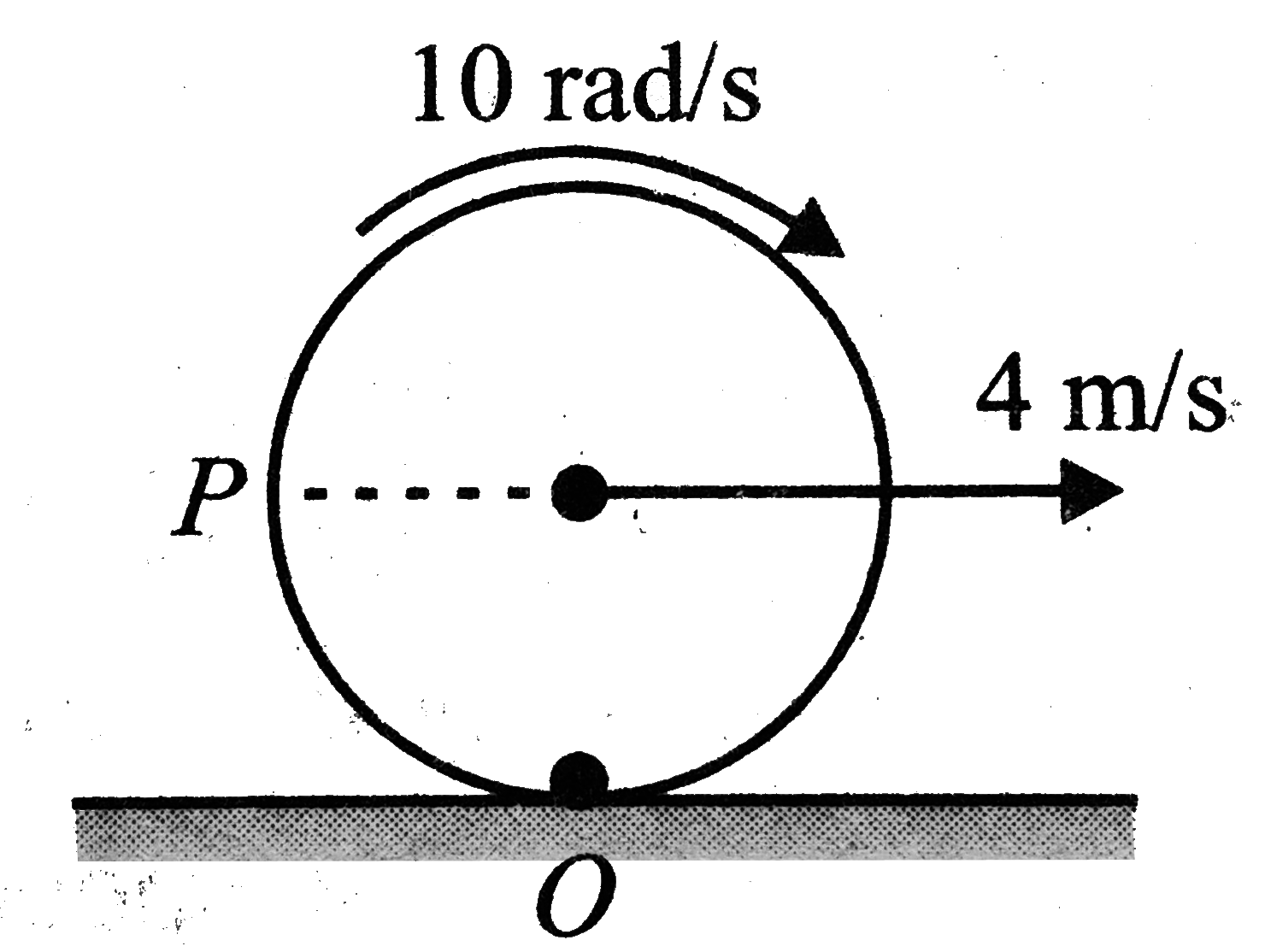
A disc of radius `20 cm` is rolling with slipping on a flat horizontal surface. At a certain instant the velocity of its centre is `4 m//s` and its angular velocity is `10 rad//s`. The lowest contact point is `O`.

Velocity of point `P` is

A disc of mass 100 g is rolling without slipping on a horizontal surface with a velocity of 10 cm s^(-1) . Calculate its total energy.

A disc of radius 0.2 m is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is O and centre of disc is C )

A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v . Find the velocity of points A , B , C and D .

A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?

A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is

A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is .

A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : at the upper most point

A uniform disc is rolling on a horizontal surface. At a certain instant B is the point of contact and A is at height 2 R from ground, where R is radius of disc - .

A disc of radius 10cm is moving with its centre's velocity =1m/s rightwards,on a flat horizontal surface.At a certain moment,its angular velocity is, 20rad/s ,anticlockwise.Then, the distance of a point on the disc (from its centre) whose instantaneous velocity is zero is

A wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v . The velocity of a particle at the highest point of the rim is