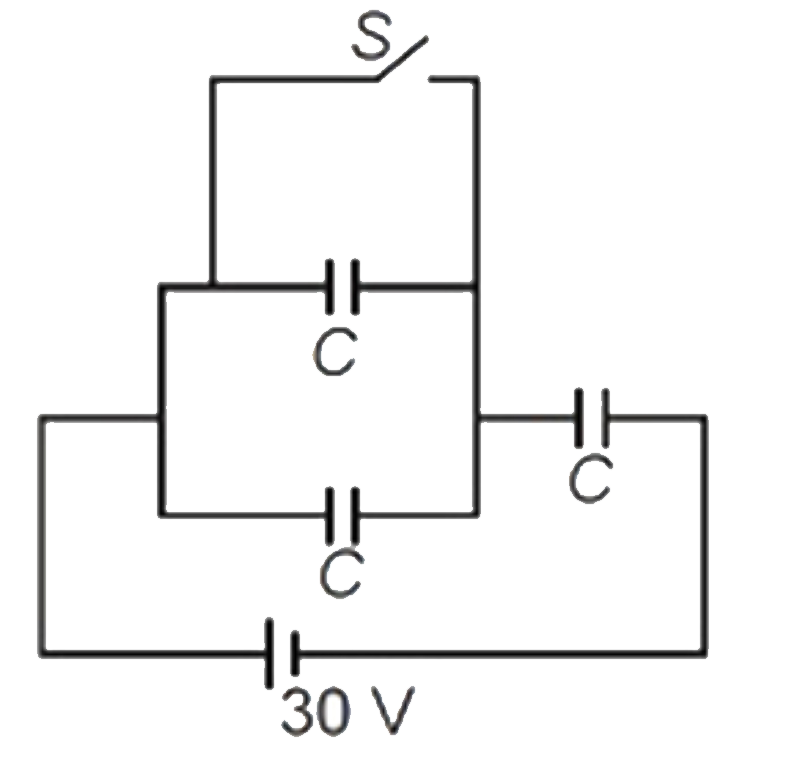
Three capacitors each of capacitance `C = 2muF` are connected with a battery of emf 30 V as shown in the figure . When the switch S is closed , the heat generated in the circuit will be

Three capacitors each having capacitance C=2 muF are connected with a battery of emf 30 V as shown in. when the switch S is closed, find a. the amount of charge flowing through the battery , b. the heat generated in the circuit, c. the energy supplied by the battery, d. the amount of charge flowing through the switch S. .

Two capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

Three capacitors of capacitances 2muF, 2muF and 4muF are connected to a battery of 10V as shown in the figure. Calculate the effective capacitance of the circuit and charge on each capacitor.

Six capacitors each of capacitance of 2muF are connected as shown in the figure. The effective capacitance between A and B is:

Three capacitors (of capacitances C , 2C and 3C ) and three resistors (of resistance R , 2R and 3R ) are connected with a battery and switch S as shown in the figure. When switch S is open, charges on the capacitors are shown. Switch S is closed at t=0 sec . The time constant of the circuit will be

An uncharged capacitor of capacitance C is connected with a battery of EMF V and a resistance R. The switch is closed at t=0 . The time instant at which the current in the circuit is (V)/(4R) is t=

Two spheres of radii R and 2R are charged to potential V0 and 2 V0 and are connected by a battery of emf V0 as shown in figure. When switch 'S' is closed then

A circuit consists of three identical lamps connected to a battery as shown in the figure. When the switch S is closed then the intensities of lamps A and B

Four capacitors of capacitances 2 muF and 1muF are connected across a battery of 10V as shown in the figure (q). Calculate the net capacitance of the combination and net charge across each capacitor.