Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMILARITY
TARGET PUBLICATION|Exercise Practice Set 1.1|8 VideosSIMILARITY
TARGET PUBLICATION|Exercise Practice Set 1.2|11 VideosSIMILARITY
TARGET PUBLICATION|Exercise Chapter Assessment|17 VideosQUESTION FROM STD. IX
TARGET PUBLICATION|Exercise Statistics|11 VideosSTATISTICS
TARGET PUBLICATION|Exercise Problem Set-6|5 Videos
Similar Questions
Explore conceptually related problems
TARGET PUBLICATION-SIMILARITY -Textual Activity
- Draw a Delta ABC. 1. Bisect angleB and name the point of intersectio...
Text Solution
|
- Draw three parallel lines. i. Label them as l, m, n. ii. Draw tran...
Text Solution
|
- In the adjoining figure, AB abs() CD abs() EF. If AC = 5.4, CE = 9, BD...
Text Solution
|
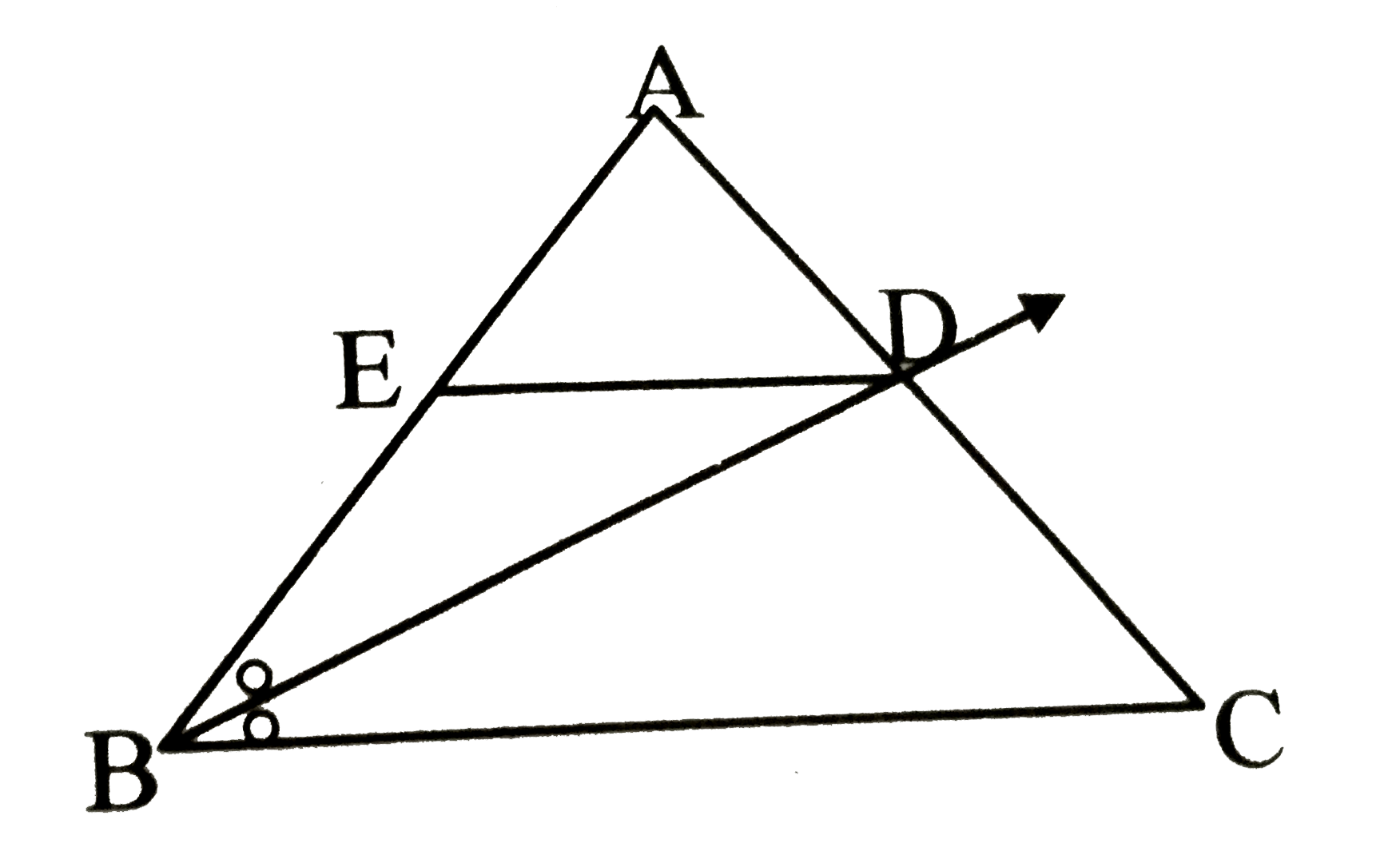
- In Delta ABC, ray BD bisects angleABC. A-D-C, side DEabs()side BC, A-E...
Text Solution
|