Home
Class 10
MATHS
In the adjoining figure, seg EF is the d...

In the adjoining figure, seg EF is the diameter of the circle with centre H. Line DF is tangent at point F. If r is the radius of the circle, then prove that `DE xxGE=4r^2`.

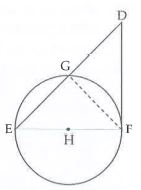
Text Solution

Verified by Experts

The correct Answer is:
`thereforeDEtimesGE=4r^2`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    TARGET PUBLICATION|Exercise Problem Set-3|23 Videos

  • CIRCLE

    TARGET PUBLICATION|Exercise Activities for Practice|3 Videos

  • CIRCLE

    TARGET PUBLICATION|Exercise Practice Set 3.4|5 Videos

  • CHALLENGING QUESTIONS

    TARGET PUBLICATION|Exercise CHAPTER-1 :Linear Equations in Two Variable|1 Videos

  • CO-ORDINATE GEOMETRY

    TARGET PUBLICATION|Exercise CHAPTER ASSESSMENT|15 Videos

Similar Questions

Explore conceptually related problems

In the adjoining figure, point A is the center of the circle. AN=10 cm. Line NM is tangent at M. MN=5 cm. Find the radius.

In the adjoining figure, seg RS is the diameter of the circle with centre 'O'. Point T is in the exterior of the circle. Prove that /_RTS is an acute angle.

In the adjoining figure, M is the centre of the circle and seg KL is a tangent. If MK=12, KL=6 sqrt 3 , then find the radius of the circle.

In the adjoining figure, the radius of a circle with centre C is 6 cm. Line AB is a tangent at A. What is the distance of point C from line AB?

In the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of angleACB intersects the circle at point D. Prove that ,seg ADcongseg BD .

In the adjoining figure, the radius of a circle with centre C is 6 cm. Line AB is a tangent at A. What the measure of /_CAB ? Why?

In the following figure ,Point A is the centre of the circle. Line MN is tangent at point M. IF AN=12cm and MN=6cm, determine the radius of the circle.

In the adjoining figure, the radius of a circle with centre C is 6 cm. Line AB is a tangent at A. d(A,B)=6 cm, find d(B,C).

In the adjoining figure, BC is a diameter of the circle with centre M. PA is a tangent at A from P, which is a point on line BC. AD bot BC prove that DP^(2)=BPxxCP-BDxxCD

In the adjoining figure, seg AB is a diameter of a circle with centre O. Bisector of inscribed /_ACB intersects circle at point D. prove: seg AD~=seg BD