A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
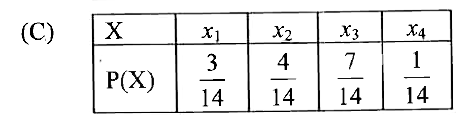
- Let X be a random variable which assumes values x1, x2, x3,\ x4 such...
Text Solution
|
- Let x1,x2 be the roots of the equation x^2-3x+A=0 and x3,x4 be those o...
Text Solution
|
- If (xi , 1/xi), i = 1, 2, 3, 4 are four distinct points on a circle, t...
Text Solution
|
- Let f(x1,x2,x3,x4)=x1^2+x2^2+x3^2+x4^2-2(x1+x2+x3+x4)+10 and x1,x3 i...
Text Solution
|
- If the normals at the four points (x1,y1),(x2,y2),(x3,y3) and (x4,y4) ...
Text Solution
|
- IF A=[{:(-1,3),(4,2):}],B=[{:(2,1),(3,-5):}],X=[{:(x1,x2),(x3,x4):}] a...
Text Solution
|
- Let x1, x2, x3 be the roots of equation x^3-x^2+beta x+gamma=0. If , x...
Text Solution
|
- A=[(-1,3),(4,2)], B =[(2,1),(3,-5)] మరియు X=[(x1, x2), (x3,x4)], A+B ...
Text Solution
|
- Let X be a random variable which assumes values x1, x2, x3,\ x4 such t...
Text Solution
|