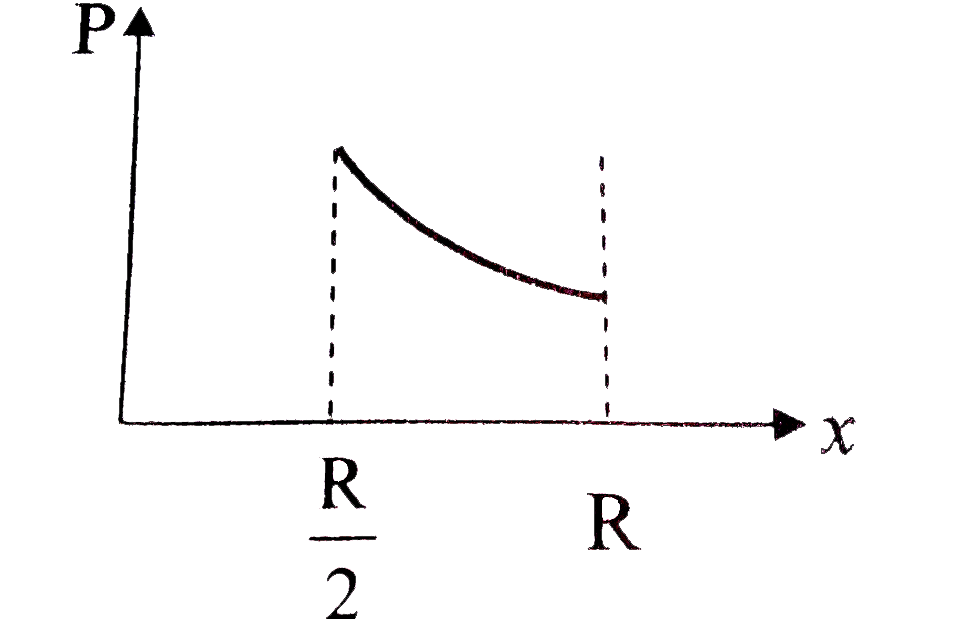
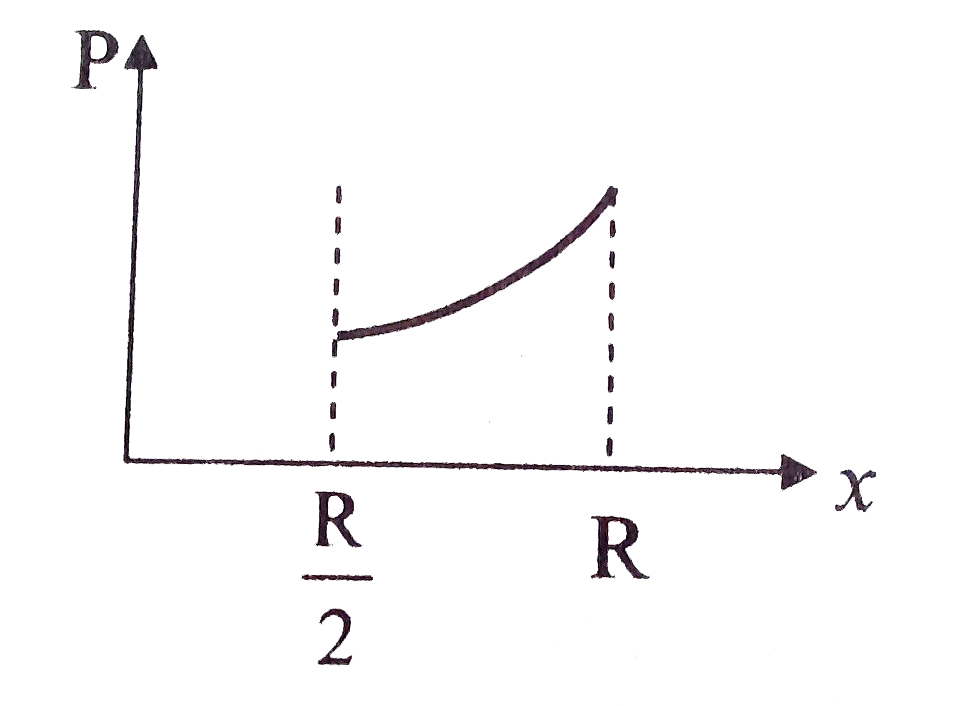
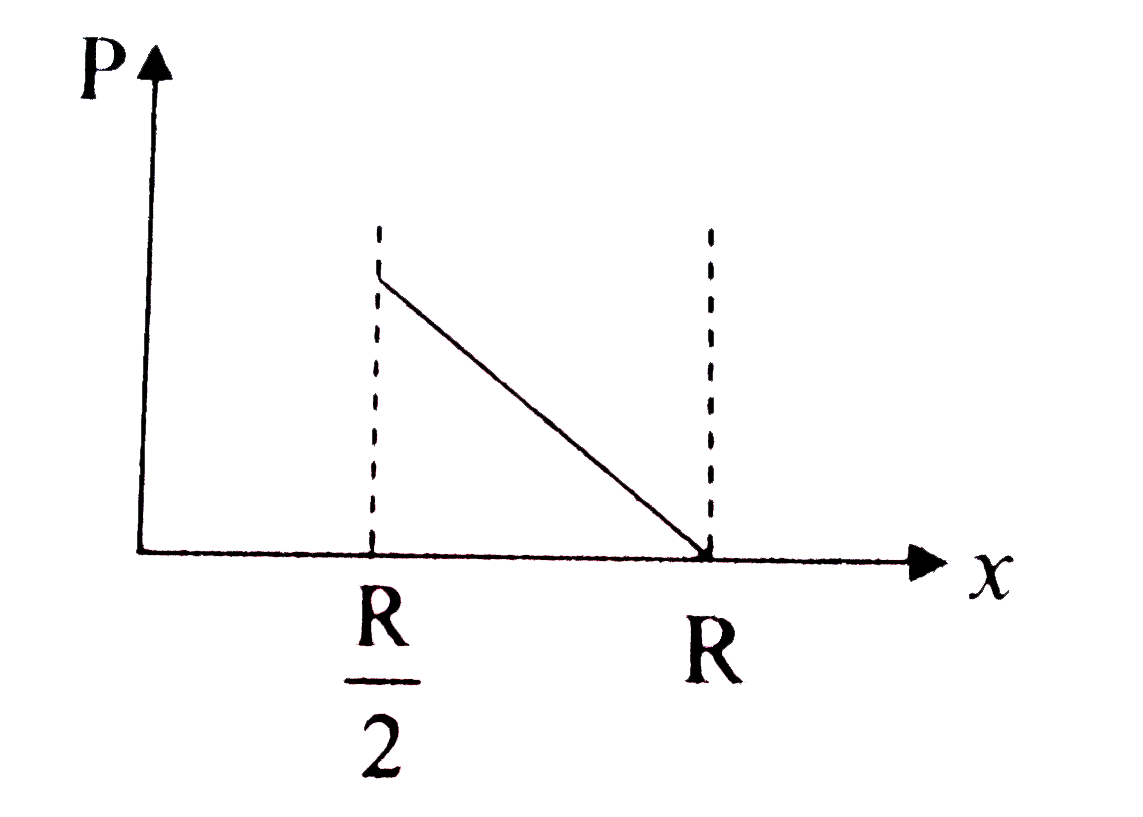
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A tunnel is dug along a chord of the earth at a perpendicular distance...
Text Solution
|
- A tunnel is dug along a diameter of the earth. Find the force on a par...
Text Solution
|
- A tunnel ois dug along a chord of the earth a perpendicular distance R...
Text Solution
|
- A tunnel is dug along a chord of the earth at a perpendicular distance...
Text Solution
|
- Assume that a tunnel is dug along a chord of the earth, at a perpendic...
Text Solution
|
- (a) A tunnel is dug along a diameter of the earth. Find the force on t...
Text Solution
|
- A tunnel is dug along a diameter of the earth. Find the force in on a ...
Text Solution
|
- A tunnel is dug along a chord of the earth a perpendicular distance R/...
Text Solution
|
- A tunnel is dug along the diameter of the earth. The gravitational for...
Text Solution
|