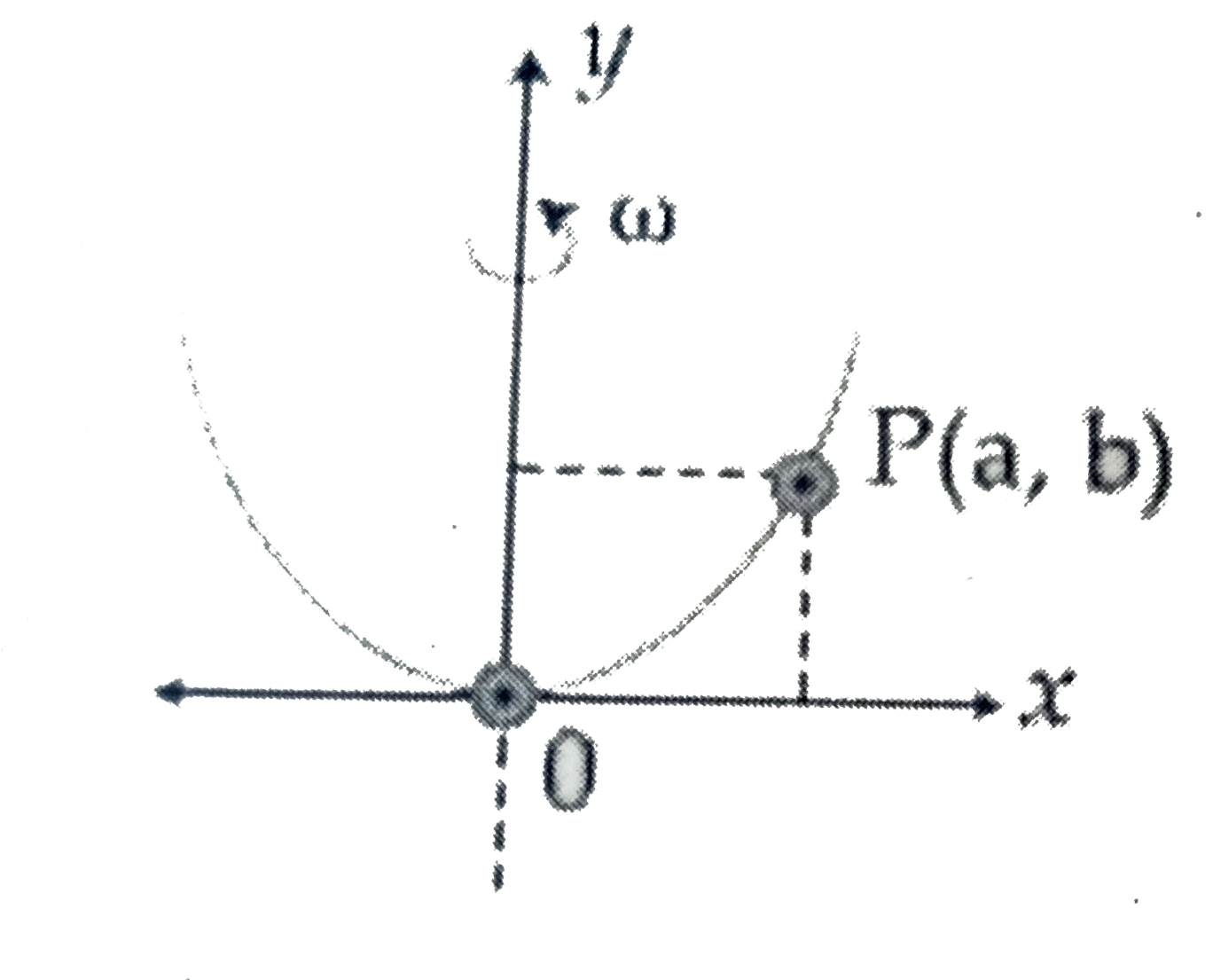
A bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola `y =4 Cx^(2)` and rotating with angular speed `omega` (see figure ) . The value of `omega` is (neglect friction),

A thin circular ring of mass per unit length p and radius r is rotating at an angular speed omega as shown in figure. The tension in the ring is

A disc of mass m and radius R rotating with angular speed omega_(0) is placed on a rough surface (co-officient of friction =mu ). Then

A smooth wire frasme is in the shape of a parabola y = 5x^(2) . It is being rotated about y-axis with an angular velocity omega . A small bead of mass (m = 1 kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity omega is (g = 10 m//s^(2))

A piece of wire is bent in the shape of a parabola y = Kx^(2) (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is

A piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:

A bead of mass m can move without friction along a long wire bent in a vertical plane in the shape of a graph of a certain function. Let l_(A) be the length of the segment of the wire from the origin to a certain point A. It is knonw that if the bead is released at point A such that l_(A) lt l_(A_(0)) , its motion will be strictly harmonic l (t) = l_(A) cos omega t . Prove that there exists a point B (l_(A_(0)) lt lt l_(B)) at which the condition of harmonicity of oscillations will be violated.

A body Is placed on a turntable. The friction coefficient between the body and the table is mu . (a) If turntable rotates at constant angular speed omega , find the maximum value of omega for which the block will not slip. (b) if the angular speed is increased uniformly from rest with an angular acceleration alpha , at what speed will the block slip?

A small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed omega about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance (a)/(2) from xy. Then is equal to:

A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity omega as shown in the figure. The rod maintains a constant angle theta with the vertical. What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m , omega , l and theta .