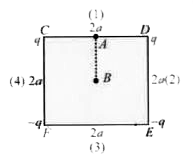
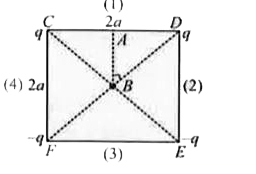
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MODEL TEST PAPER 1
MTG-WBJEE|Exercise PHYSICS (Category) 3 : Single Option correct type (2 mark) |5 VideosMODEL TEST PAPER 1
MTG-WBJEE|Exercise PHYSICS (Category) 3 : Single Option correct type (2 mark) |5 VideosMAGNETICS
MTG-WBJEE|Exercise WB JEE Previous Years Questions (Category 3: One or More than one Option)|2 VideosMODEL TEST PAPTER
MTG-WBJEE|Exercise MCQs|80 Videos
Similar Questions
Explore conceptually related problems
MTG-WBJEE-MODEL TEST PAPER 1 -PHYSICS (Category) 2 : Single Option correct type (2 mark)
- Two positive charges of magnitude q are placed at the ends of a side (...
Text Solution
|
- Water of volume 2 liter in a container is heated with a coil of 1 kW ...
Text Solution
|
- The relation between U,P and V for an ideal gas in an adiabatic proce...
Text Solution
|
- The simplified Y output of the given logic circuit is
Text Solution
|
- A 1000 kg elevator rises from rest in the basement to the fourth floo...
Text Solution
|