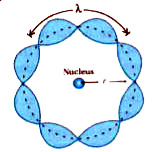
Text Solution
Verified by Experts
Topper's Solved these Questions
ATOMS
KUMAR PRAKASHAN|Exercise TRY YOURSELF |43 VideosATOMS
KUMAR PRAKASHAN|Exercise SECTION-B (NUMERICALS) (Numerical From Textual Illustrations)|9 VideosALTERNATING CURRENTS
KUMAR PRAKASHAN|Exercise SECTION-D MCQs (COMPETITIVE EXAMS)|64 VideosBOARD'S QUESTION PAPER MARCH-2020
KUMAR PRAKASHAN|Exercise PART-B SECTION -C|4 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-ATOMS-Section-D -MCQs asked in GUJCET / Board Exam
- Explain the quantization of angular momentum to behave an electron as ...
Text Solution
|
- The ratio of longest wavelength and the shortest wavelength observed i...
Text Solution
|
- Which line of the Balmer series has the maximum wavelength ?
Text Solution
|
- As the quantum number increases, the difference of energy between cons...
Text Solution
|
- In Rutherford's alpha-scattering experiment, what will be the correct ...
Text Solution
|
- The potential energy of the orbital electron in the ground state of hy...
Text Solution
|
- What will the angular momentum in fourth orbit, if L is the angular mo...
Text Solution
|
- The ratio of areas of the electron orbits for the first excited state ...
Text Solution
|
- What is the difference of angular momenta of an electron between two c...
Text Solution
|
- The ratio of kinetic energy of the total energy of an electron of a Bo...
Text Solution
|
- The potential difference applied to an X-ray tube is 5 kV and the curr...
Text Solution
|
- For an electron in the second orbit of Bohr's hydrogen atom, the momen...
Text Solution
|
- of the following transitions in the hydrogen atom, the one which gives...
Text Solution
|
- The relation between principle quantum number (n) and orbital radius (...
Text Solution
|
- The total energy of an electron in second excited state is - 2E. What ...
Text Solution
|
- The atom of hydrogen absorbs 12.75 eV of energy in ground state. Then ...
Text Solution
|
- Find out the atomic number of the element which gives X-ray of minimum...
Text Solution
|
- The minimum wavelength of the X-rays produced by electrons accelerated...
Text Solution
|
- Write range of wave length of X - rays.
Text Solution
|
- If , lambda(1) and lambda(2) are the wavelength of the numbers of th...
Text Solution
|
- Number of spectral line of hydrogen atom is
Text Solution
|