Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
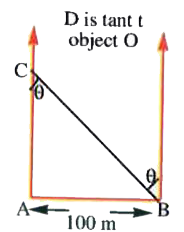
- A man wishes to estimate the distance of a nearby tower from him. He s...
Text Solution
|
- A man wishes to estimate the distance of a nearby tower from him. He s...
Text Solution
|
- किसी टावर के पाद से 160 मी . दूर स्थित बिंदु से टावर का उन्नयन कोंढ ...
Text Solution
|
- एक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी का आकलन करना चाहता ह...
Text Solution
|
- एक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी आकलन करना चाहता है। ...
Text Solution
|
- A man standing at a point P is watching the top of elevation of 30^@. ...
Text Solution
|
- A man wishes to estimate the distance of a nearby tower from him. He s...
Text Solution
|
- A man wishes to estimate the distance of a nearby tower from him. He s...
Text Solution
|
- A man wishes to estimate the distance of a nearby tower from him. He s...
Text Solution
|