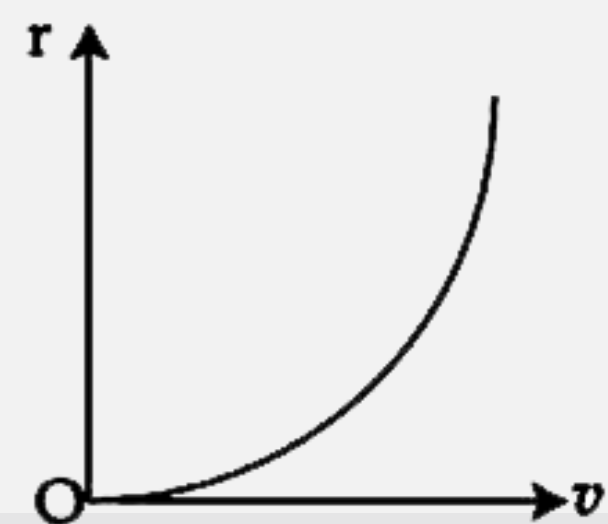
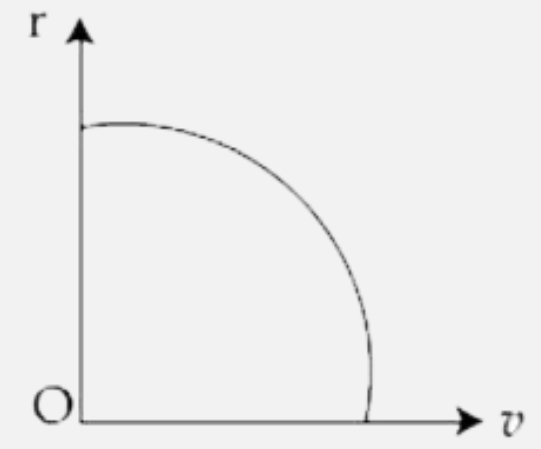
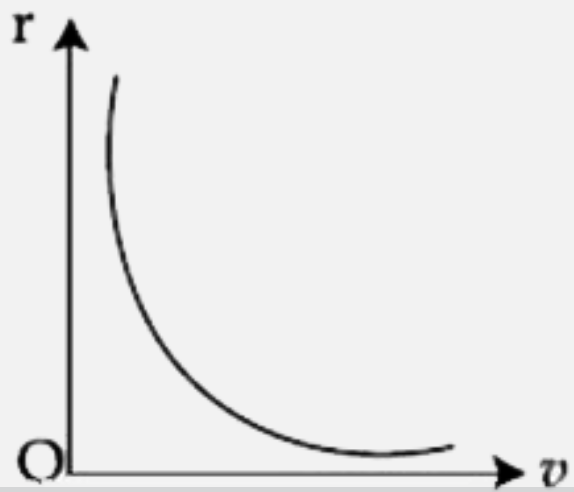
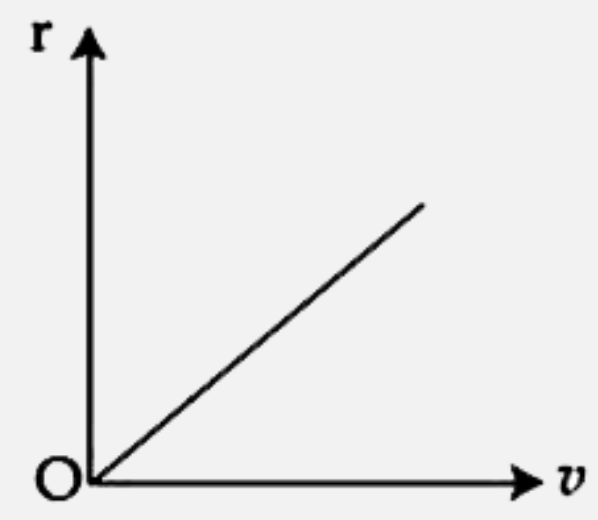
A
B
C
D
Text Solution
AI Generated Solution
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass m moves in a circular orbit under the central poten...
Text Solution
|
- According to the Bohr-Sommerfeld postulate the periodic motion of a pa...
Text Solution
|
- A small particle of mass m moves in such a way that the potential ener...
Text Solution
|
- A particle of mass 3 kg is moving under the action of a central force ...
Text Solution
|
- A body moves in a circular orbit of radius R under the action of a cen...
Text Solution
|
- A particle of mass 9 kg is moving under the action of a central force ...
Text Solution
|
- A particle of mass m moves in a circular orbit in a central potential ...
Text Solution
|
- m द्रव्यमान का एक कण r त्रिज्या के एक क्षैतिज वृत्तीय मार्ग पर गति...
Text Solution
|
- A test particle is moving in a circular orbit in the gravitational fie...
Text Solution
|