Text Solution
Verified by Experts
Topper's Solved these Questions
SUPERPOSITION OF WAVES
DC PANDEY ENGLISH|Exercise Level 2 Single Correct|15 VideosSUPERPOSITION OF WAVES
DC PANDEY ENGLISH|Exercise Level 2 More Than One Correct|6 VideosSUPERPOSITION OF WAVES
DC PANDEY ENGLISH|Exercise Level 1 Subjective|24 VideosSOUND WAVES
DC PANDEY ENGLISH|Exercise Exercise 19.7|4 VideosTHERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
DC PANDEY ENGLISH|Exercise Medical entrance gallary|30 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-SUPERPOSITION OF WAVES-Subjective Questions
- A thin taut string tied at both ends and oscillating in its third harm...
Text Solution
|
- A 160 g rope 4 m long is fixed at one end and tied to a light string o...
Text Solution
|
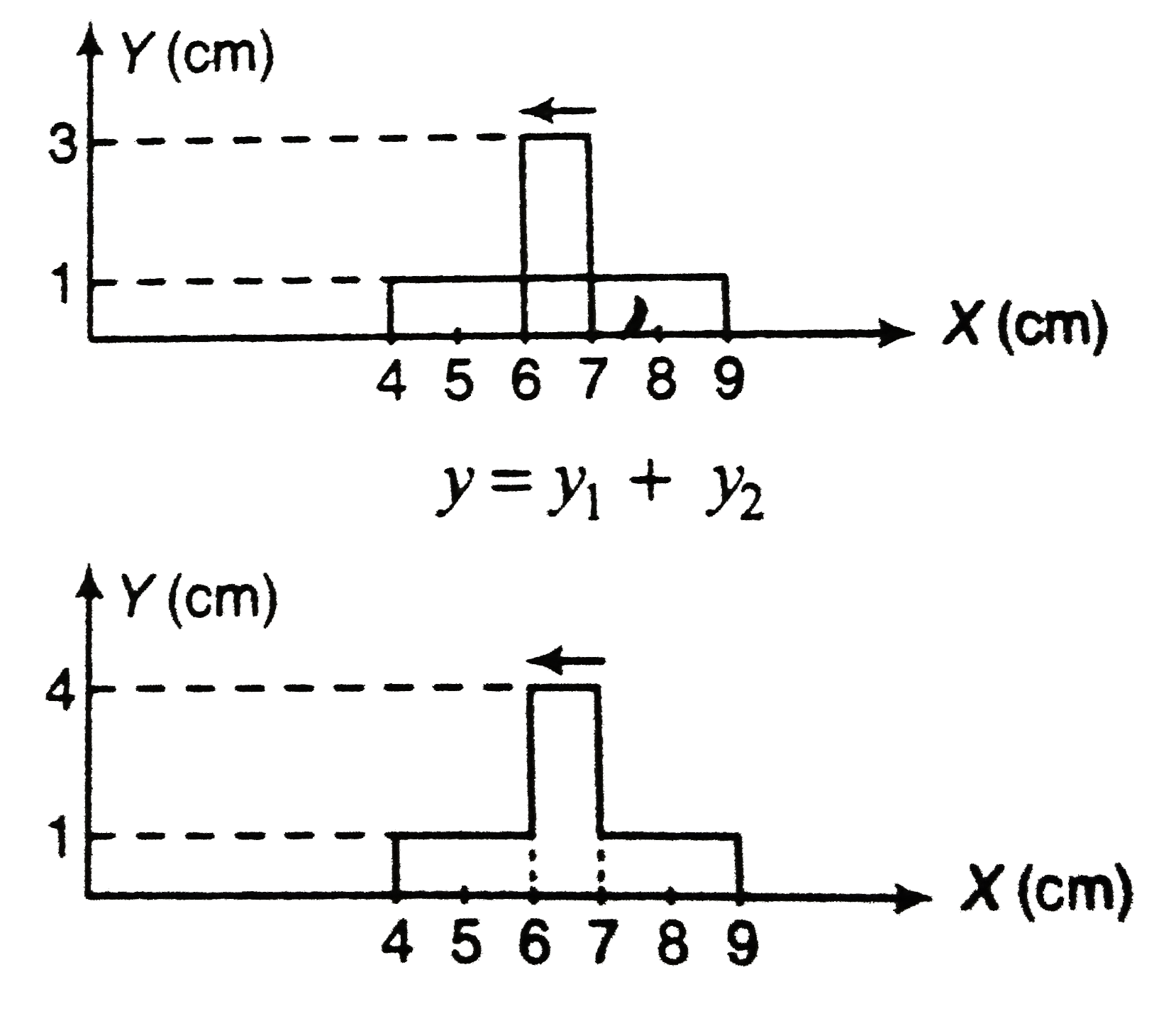
- Two pulses travelling in opposite directions along a string are shown ...
Text Solution
|
- Sources separated by 20 m vibrate according to the equation y1 = 0.06s...
Text Solution
|
- Three component sinusoidal waves progressing in the same directions al...
Text Solution
|
- A metal rod of length 1m is clamped at two points as shown in the figu...
Text Solution
|