A straight segment `OC` (of lengh `L`) of a circuit carrying a current I is placed along the x-axis. Two infinitely long straight wire `A` and `B` each extending from `z=-ooto+oo` are fixed at `y=-a` and `y=+a` respectively as show in the figure. If the wires `A` and `B` each carry a current I into the plane of the paper, obtain the expression for the force acting on the segment `OC`. What will be the force on `OC` if the current in the wire `B` is reversed?

Explanation

a. Let us assume a segment of wire `OC` at a point `P`, a distance `x` from the centre d length `dx` as shown in figure.

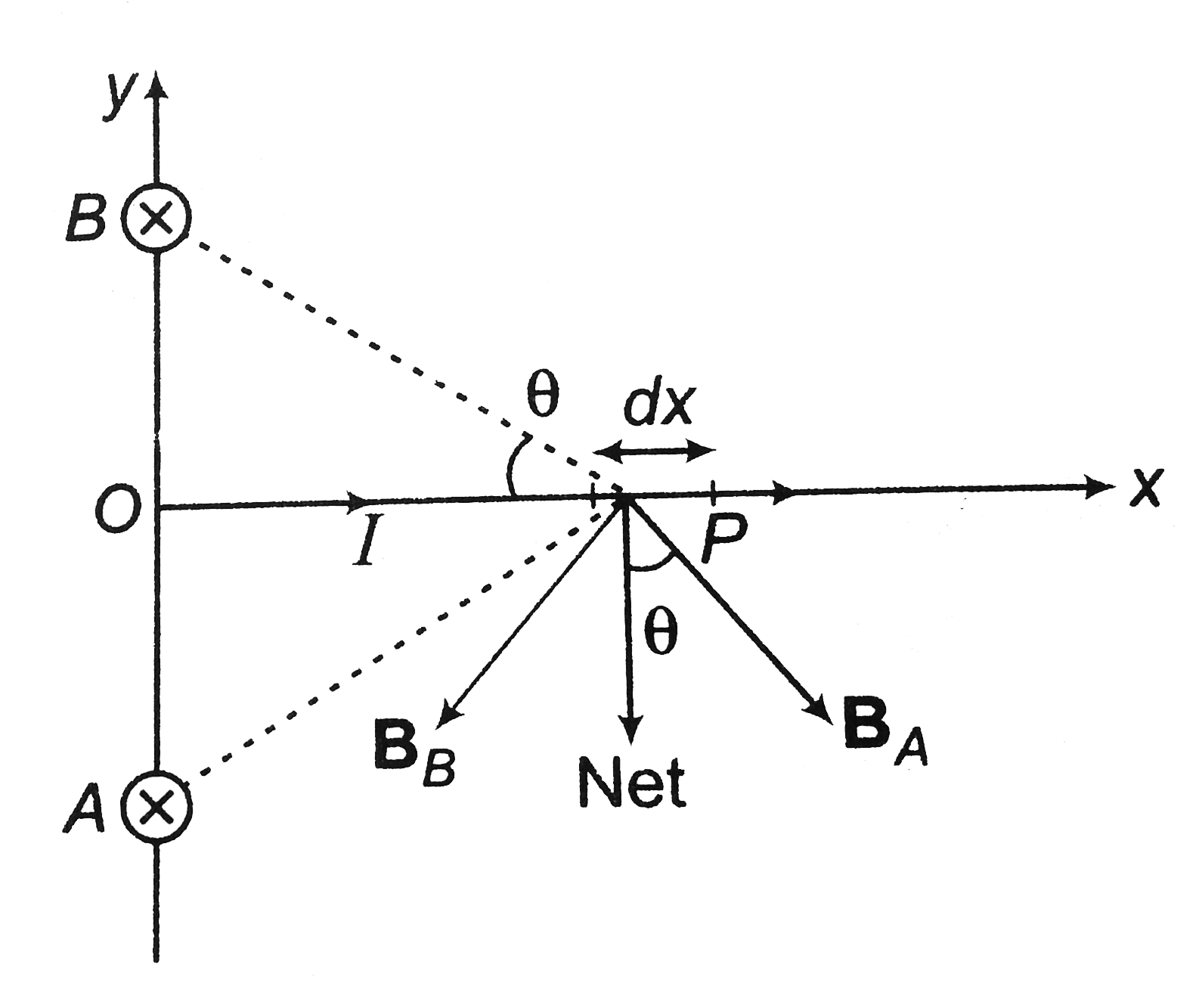
Magnetic field at `P` due to current in wires `A` and `B` will be in the directions perpendicular to `AP` and `BP` respectively as shown.
`|B|=(mu)/(2pi) I/(AP)`
therefore, net magnetic force at `P` will be along negative y-axis as shown below
`B_("net")=2|B|costheta`
`=2(mu_0/(2pi))I/(AP)(x/(AP))`
`B_("net")=(mu_0/pi)=(Ix)/((AP)^2)`
`B_("net")=(mu)/(pi)(Ix)/((a^2+x^2))`

Therefore, force on this element will be
`dF=I{(mu_0)/(pi)I(x)/(a^2+x^2)}dx` [in negative z-direction]
`:.` total force on the wire will be
`F=int_(x=0)^(x=L)` `dF(mu_0I^2)/piint_0^L(xdx)/(x^2+a^2)`
`=(mu_0I^2)/(2pi) ln (L^2+a^2)/(a^2)` [in negative z-axis]
Hence, `F=-(mu_0I^2)/(2pi) ln ((L^2+a^2)/a^2)hatk`
b. When direction of current in `B` is reversed net magnetic field is a along the current. Hence force is zero