A wire loop carrying a current `I` is placed in the `xy`-plane as shown in figure

a. If a particle chsarge +Q and mass m is placed at in centre `P` and given a velocity `v` along `NP` (see figure), find its instaneous acceleration.
If an external uniform magnetic induction field `B=Bhati` is applied, find the force and the torque acting on the loop due to this field.

Explanation

a. Magnetic field at `P` due ot arc of circle

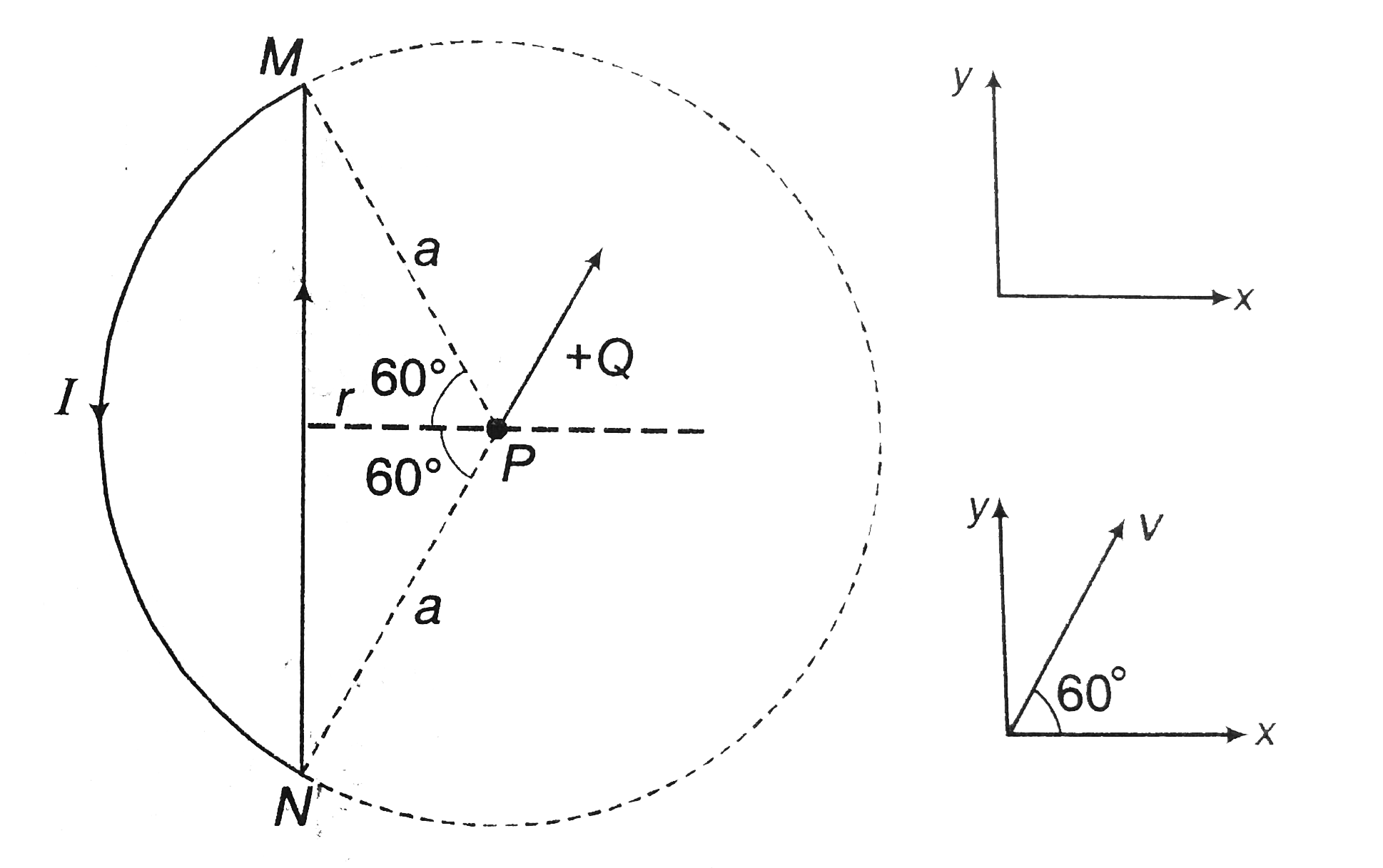
Subtending and angle of `120^@` at centre would be
`B_1=1/3("field due to circle")=1/3((mu_0I)/(2a))`
`=(mu_0I)/(6a)` [outwards]
`=(0.16mu_0I)/a` [outwards]
`B_1=(0.16mu_0I)/ahatk`
Magnetic field due to straight wire `NM` at P
`B_2=mu_0/(4pi) I/r(sin60^@+sin60^I@)`
here `racos60^@`
`:. B_2=mu_0/(4pi) I/(acos60^@)(2sin 60^@)`
or `B_2mu_0/(2pi) I/ tan 60^@`
`=(0.27mu_0I)/(a) ("inward")`
or`B_2=-(0.27mu_0I)/ahatk`
`:. B_(net)=B_1+B_2=-(0.11mu_0I)/ahatk`
Now, velocity of particle can be written as
`v=vcos60^@hati+vsin60^@hatj`
`=v/2hati+(sqrt3v)/2hatj`
magnetic force
`F_m=Q(vxxB)`
`=(0.11mu_0IQv)/(2a) hatj-(0.121sqrt3mu_IQv)/(2a) hati`
`:.` Instantaneous acceleration
`a=F_m/m=(0.11m_0IQv)/(2am)(hatj-sqrt3hati)`
b. In uniform magnetic field, force on a current loop is zero. further magnetic dipole moment of the loop will be
`M=(IA)hatk`
Here `A` is the area of the loop
`A=1/3(pia^2)-1/2[2xxasin60^@][acos60^@]`
`=pia^2/3-a^2/2sin120^I@`
`=0.61a^2`
`:. M=(0.61Ia^2)hatk`
Given, B`=`Bhati
`:. tau=MxxB=(0.61Ia^2B)hatj`