Home
Class 12
PHYSICS
Figure shows a torch producting a straig...

Figure shows a torch producting a straight light beam falling on a plane mirror at an angle `60^(@)` The reflected beam makes a spot P on the screen along y-axis . If at t=0, mirror starts ratating about the hinge A with an angular velocity `(omega)=1^(@)` per second clockwise. Find the speed of the spot on screen after time t = 15 s.

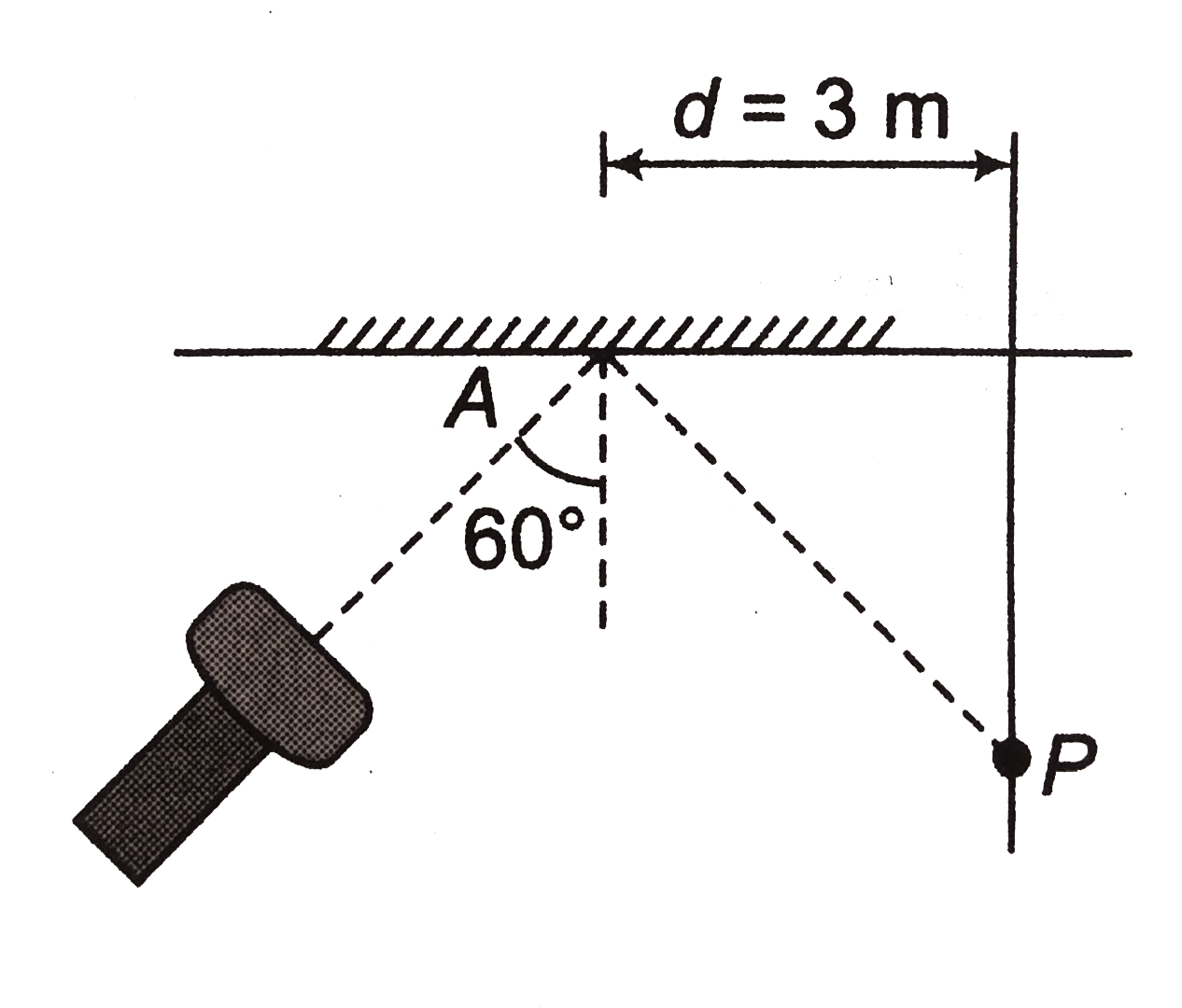
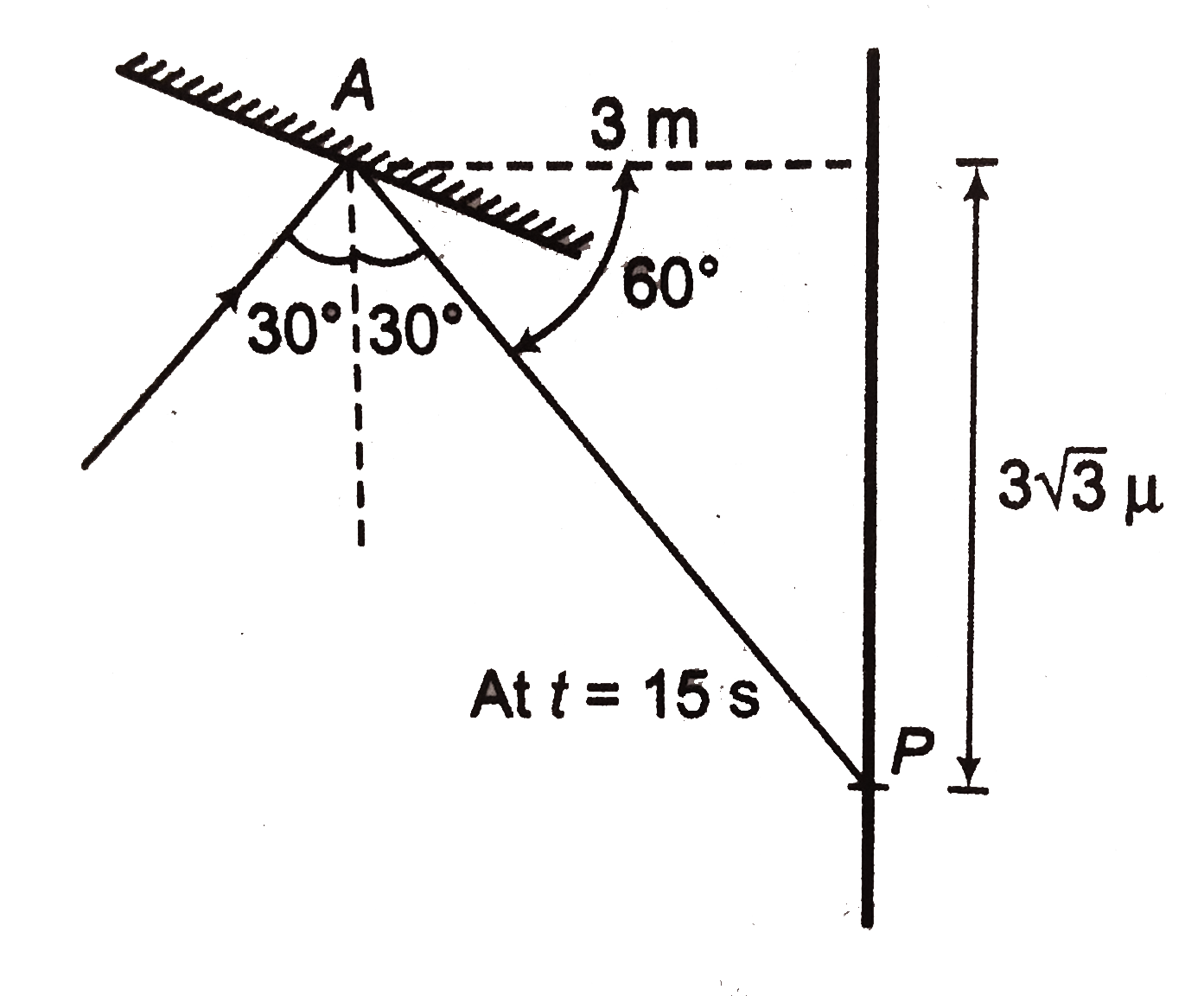
Text Solution

Verified by Experts

The correct Answer is:
A, B
In 15 second, mirror will rotate `15^(@)` in clockwise direction.
Hence, the reflected ray will rotate `(30^(@))` in clockwise direction


`y=3 tan(theta)`
` :. (dy)/(dt)=(3 sec^(2) theta).(d theta)/(dt)` ...(i)
Here, `(dy)/(dt) =(v_(p)),(d theta)/(dt) =2^(@)` per second
`=(2xxpi)/(180)=(pi)/(90)` rad per second
At `t=15 s` and `(theta)=60^(@)`
Substituting the values in Eq. (i), we have
`v_(p)={3 sec^(2) 60^(@)}{(pi)/(90)}`
`=3xx4xx(pi)/(90)`
`=(2 pi)/(15) m//s`.
Promotional Banner

Topper's Solved these Questions

  • REFLECTION OF LIGHT

    DC PANDEY ENGLISH|Exercise Level 2 Comprehensive Based|4 Videos

  • RAY OPTICS

    DC PANDEY ENGLISH|Exercise Medical entrance gallary|76 Videos

  • REFRACTION OF LIGHT

    DC PANDEY ENGLISH|Exercise Level 2 Subjective|21 Videos

Similar Questions

Explore conceptually related problems

Figure shows a torch producing a straight light beam falling on a plane mirror at an angle 60^(@) . The refected beam makes a spot P on the screen along y-axis. If at t=0 the mirror starts rotating about the hinge A with an angular velocity omega=1^(@) per second clockwise, find the speed of the spot on screen after time t=15s

Figure shows a plane mirror hinged at O and free to rotate in a vertical plane. The point O is at a distance x from a long screen. A beam of light moving vertically downwards is reflected by the mirror at O so that a bright spot P is formed at the screen. At the instant shown, the angle of incidence is theta and the mirror is rotating clockwise with constant angular veloity omega . Find the speed of spot P at this instant.

Figure shows a solid transport semi cylinder of radius 10 cm . A screen is placed at a distance 60 cm from O . A narrow beam is incident along X- axis at O . If cylinder starts rotating about O in clockwise direction with angular speed 6 rad//s spot formed on screen will move upward (Refractive index of material of cylinder =(5)/(3) ) What is initial angular velcity of ray refrected from plane surface.

The circuit shows a resistance, R=0.01Omega and inductance L=3mH connected to a conducting rod PQ of length l=1m which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuit is seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity omega =2 rad//sec . Find the magnitude of this torque (inN-m) at t=(0.3In 2) second.

A particle moves in the x-y plane with a constant acceleration of 1.5m//s^(2) in the direction making an angle of 37^(@) with the x-axis. At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.

A light ray I is incident on a plane mirror M .The mirror is rotated in the direction as shown in the figure by an arrow at frequency (9)/(pi) "rev"//"sec" ,The light reflected by the mirror is received on the wall W at a distance 10m from the axis of rotation .When the angle of incidence becomes 37^(@) find the speed of the spot (a point) on the wall?

A particle movesin the X-Y plane with a constasnt acceleration of 1.5 m/s^2 in the direction making an angle of 37^0 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity omega . (a) Find the magnitude of the horizontal force exerted by the hinge on the body. (b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.

At the centre of a fixed large circular coil of radius R a much smaller circular coil of radius r is placed .The two coils are concentric and are in the same plane .The larger coil carries a current I The smaller coil is set to rotate with a constant angular velocity omega about an axis along their common diameter .Calculate the emf induced in the smaller coil after a time t of its start of ratation

Figure shows a circuit having a coil of resistance R = 2.5 Omega and inductance L connected to a conducting rod of radius 10 cm with its center at P . Assume that friction and gravity are absent and a constant uniform magnatic field of 5 T exists as shown in figure. At t = 0 , the circuit is switched on and simultaneously a time-varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40 rad s^(-1) . Find the magnitude of this torque (in mNm ) when current reaches half of its maximum value. Neglect the self inductance of the loop formed by the circuit.