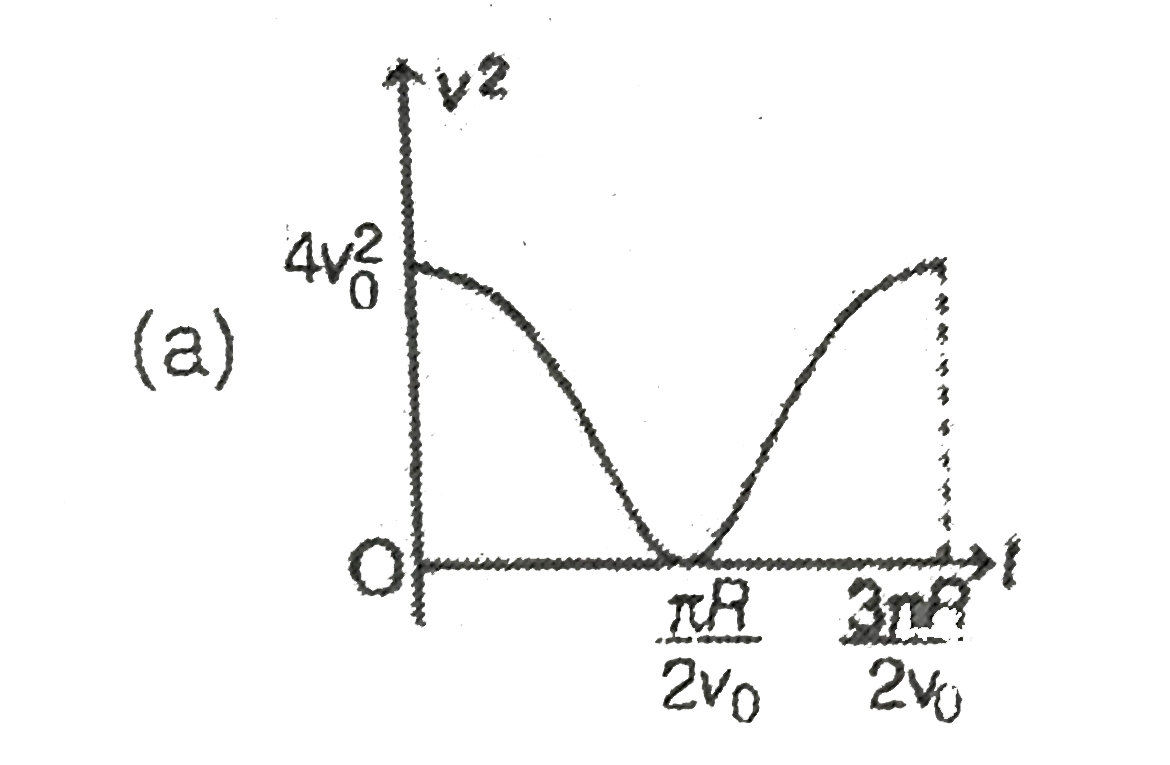
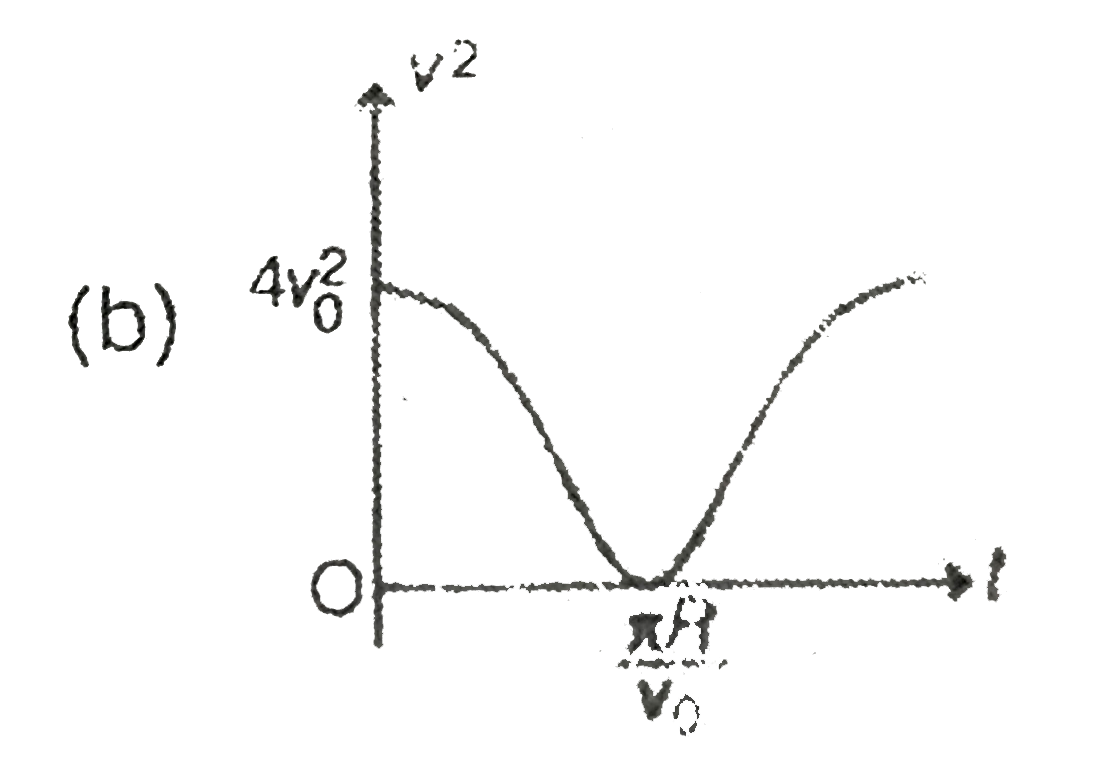
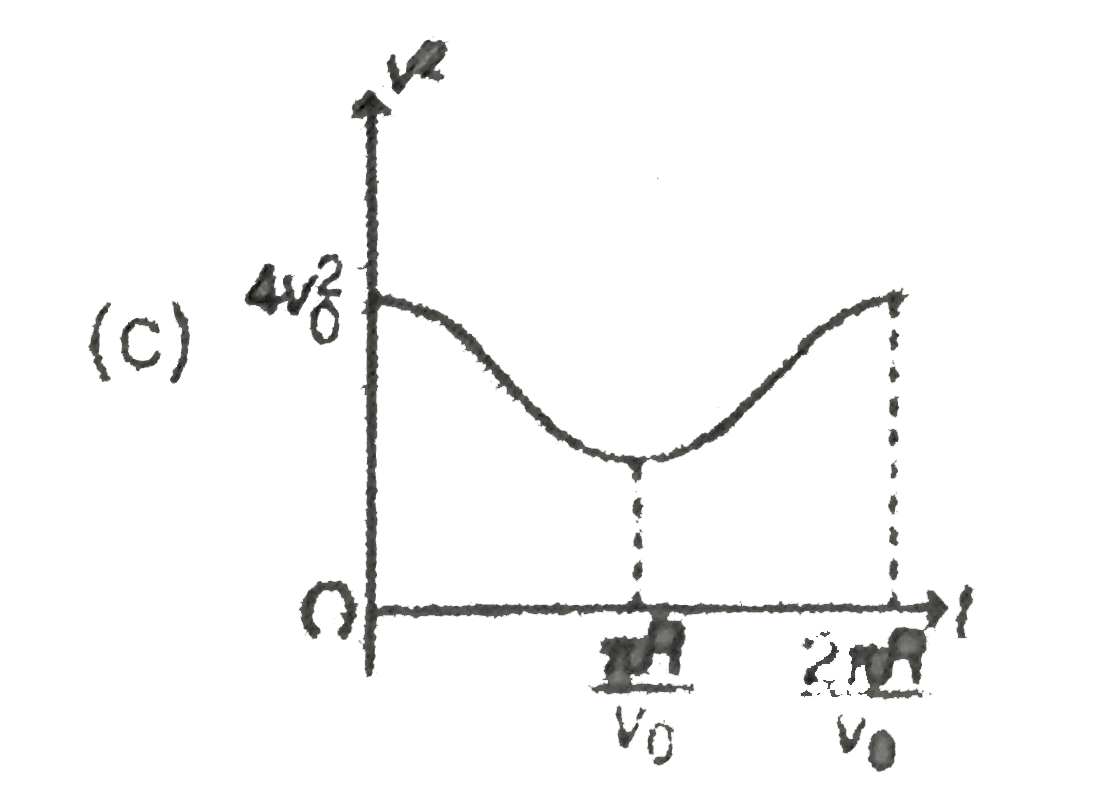
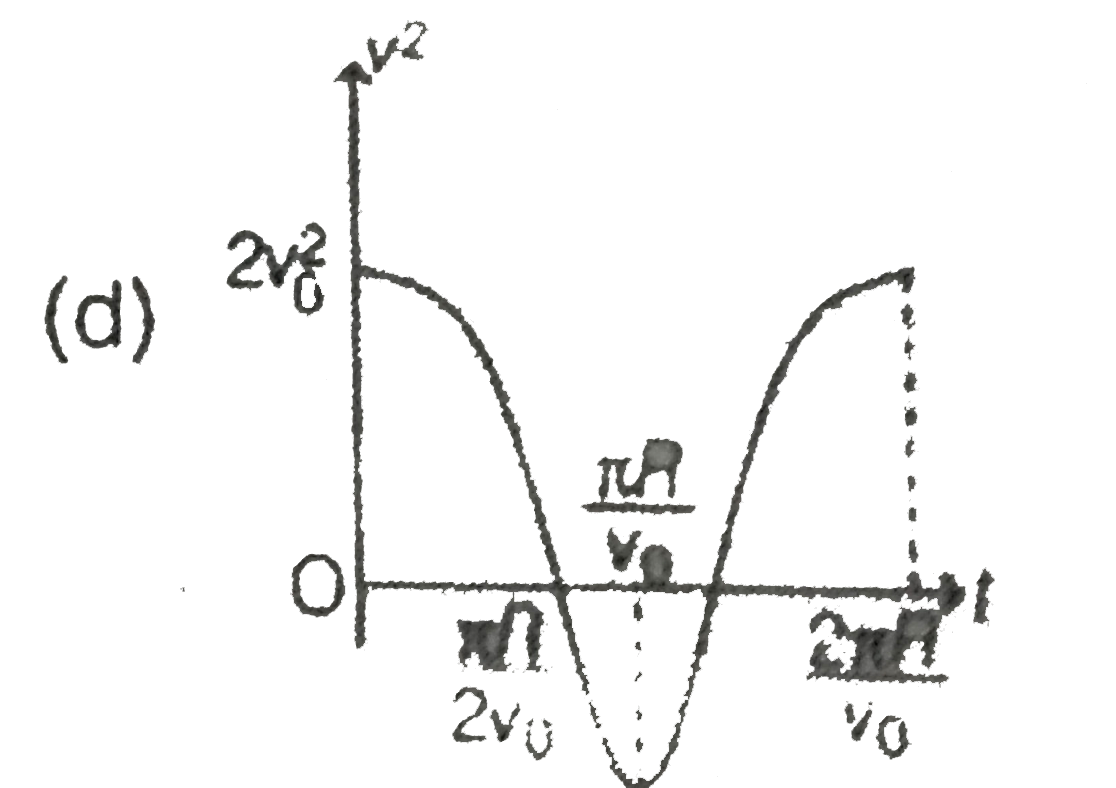
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
ROTATIONAL MOTION
DC PANDEY ENGLISH|Exercise More than one option is correct|36 VideosROTATIONAL MOTION
DC PANDEY ENGLISH|Exercise Comprehension Type Questions|40 VideosROTATIONAL MOTION
DC PANDEY ENGLISH|Exercise Integer Type Questions|17 VideosROTATIONAL MECHANICS
DC PANDEY ENGLISH|Exercise Subjective Questions|2 VideosSEMICONDUCTORS AND ELECTRONIC DEVICES
DC PANDEY ENGLISH|Exercise More than One Option is Correct|3 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-ROTATIONAL MOTION-A Only One Option is Correct
- A flat rail road car is accelerating along the positive x-axis with an...
Text Solution
|
- A uniform ring of mass m and radius R is released from top of an incli...
Text Solution
|
- A wheel ios rolling without sliding on a horizontal surface. The centr...
Text Solution
|
- a uniform circular disc of radiu8s r placed on a roughn horizontal pla...
Text Solution
|
- A solid sphere of radius R is resting on a smooth horizontal surface. ...
Text Solution
|
- Four holes of radius R are cut from a thin square plate of side 4 R an...
Text Solution
|
- Choose the correct option: A wire of mass m and length l is bent in ...
Text Solution
|
- A uniform disc of radius R lies in x-y plane with its centre at origin...
Text Solution
|
- Two rods OA and OB of equal length and mass are lying on xy plane as s...
Text Solution
|
- Choose the correct option: A wire of length l and mass m is first be...
Text Solution
|
- Choose the correct option: A disc of radius R rolls on a horizontal ...
Text Solution
|
- A rod of length l slided down along the inclined wall as shown in figu...
Text Solution
|
- A disc of radius R rolls without slipping at speed v along positive x-...
Text Solution
|
- Two particles A and B are situated at a distance d = 2m apart. Particl...
Text Solution
|
- A force F is applied on the top of a cube as shown in the figure. The ...
Text Solution
|
- A cube is pplaced on an inclined plane of inclinbation theta as shown ...
Text Solution
|
- A uniform rod AB of mass m and length l is at rest on a smooth horizon...
Text Solution
|
- Choose the correct option: A horizontal turn table in the form of a ...
Text Solution
|
- Average torque on a projectile of mass m (initial speed u and angle of...
Text Solution
|
- A uniform rod AB of mass m and length 2a is falling freely without rot...
Text Solution
|