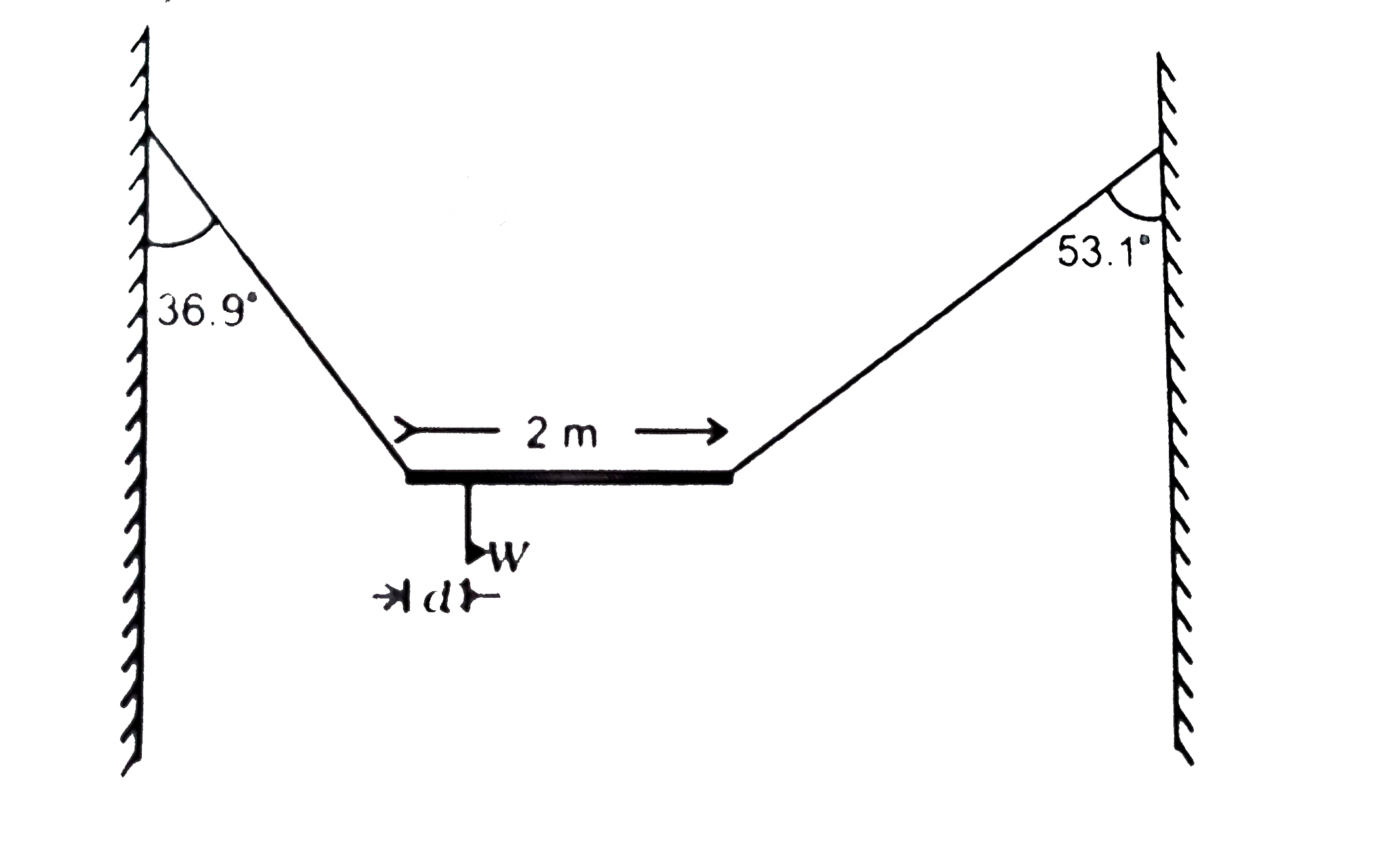
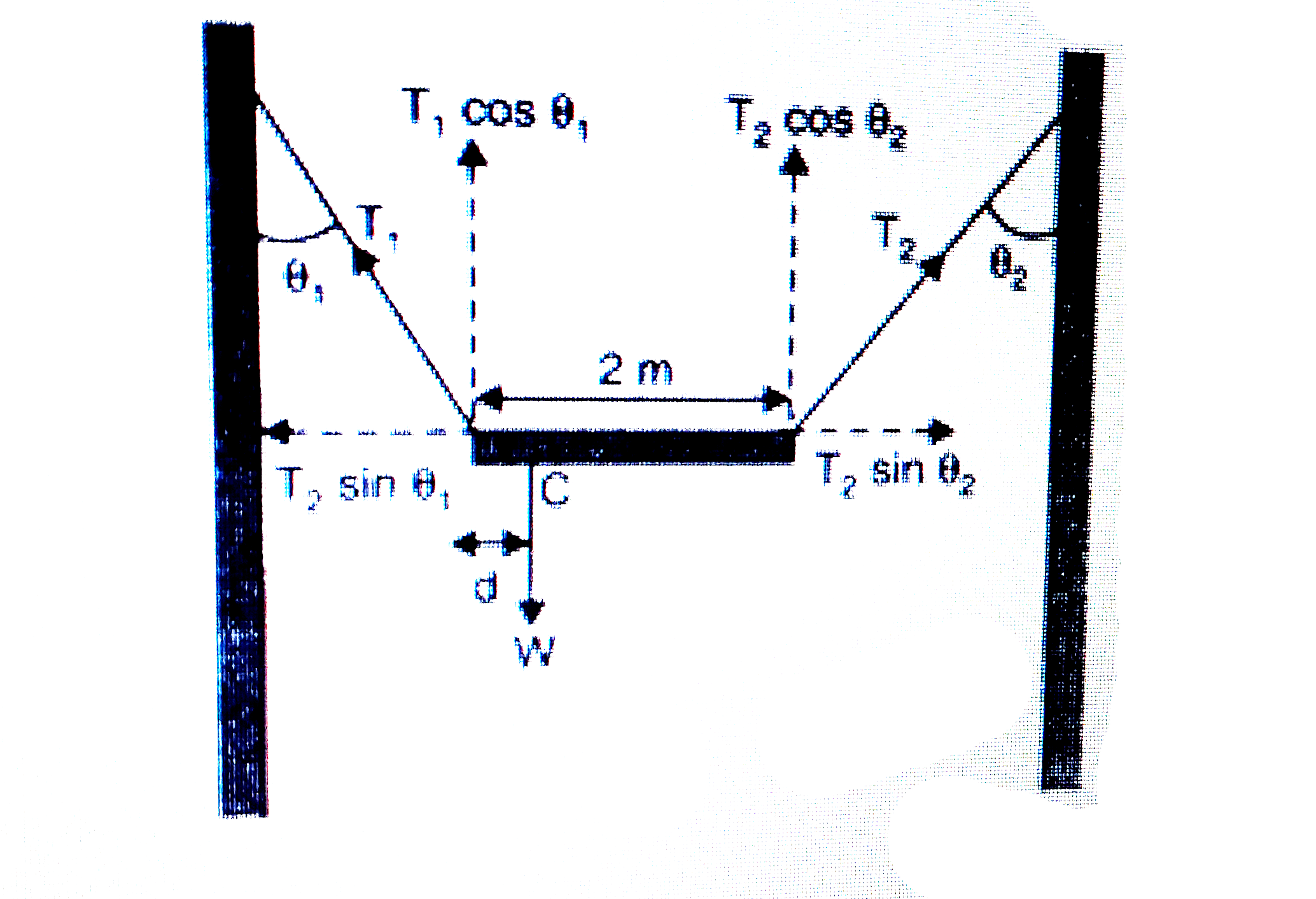A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A non-uniform bar of weight W is suspended at rest by two strings of n...
Text Solution
|
- A thin uniform bar of mass m and length 2L is held at an angle 30^@ wi...
Text Solution
|
- A non-uniform bar of weight W and weight L is suspended by two strings...
Text Solution
|
- A non-uniform bar of weight W is suspended at rest by two strings of n...
Text Solution
|
- A rigid bar AB is supported in a vertical plane and carries a load Q a...
Text Solution
|
- A non-uniform bar of weight w is suspended at rest by two strings of n...
Text Solution
|
- W भार की एक असमांग छड़ को , उपेक्षणिय भार वाली दो डोरियों से चित्र 7.39...
Text Solution
|
- A non-uniform bar of weight 'w' is suspended at rest by two strings of...
Text Solution
|
- W भार की एक असमांग छड़ को, उपेक्षणीय भार वाली दो डोरियों से चित्र में ...
Text Solution
|