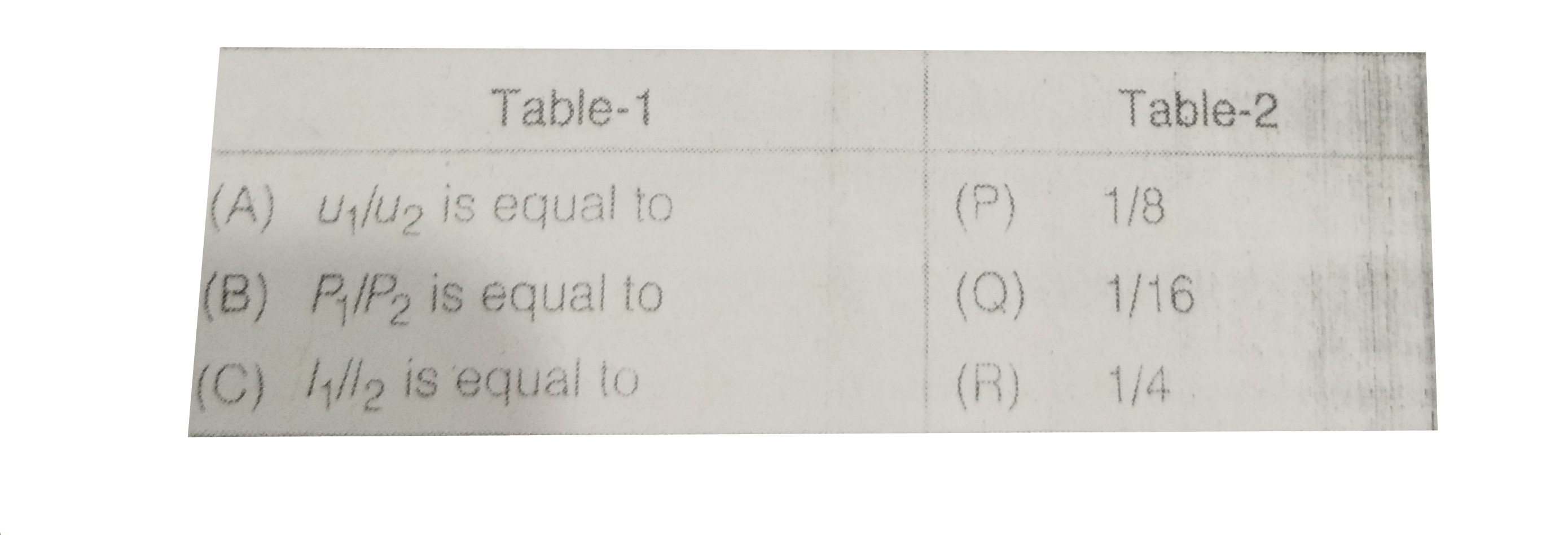Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-WAVE MOTION-Matrix Matching
- A sound source has frequency f. Source and observer both have same spe...
Text Solution
|
- In the equation ,y =A sin 2pi(ax+bt+pi//4)match the following.
Text Solution
|
- A wave is transmitted from denser to a rarer medium. Then match the fo...
Text Solution
|
- For a closed organ pipe, match the following .
Text Solution
|
- A string is suspended from the ceiling. A wave train is produced at th...
Text Solution
|
- From a single source, two wave trains are sent in two different string...
Text Solution
|
- Regarding speed of sound ingas, match the following .
Text Solution
|
- Fundamental frequency of a closed of a pipe is 100 and that of an open...
Text Solution
|
- Speed of longitudinal wave vpropsqrtE. Here, E is the modulus of elest...
Text Solution
|
- A string fixed at both ends first oscillates in its fundamental mode t...
Text Solution
|
- Following is given the equation of a travelling wave (all is SI unit) ...
Text Solution
|
- Following is given the eqution of a stationary wave (all in SI units) ...
Text Solution
|
- Match the following.
Text Solution
|
- In case of mechanical wave a particle oscillates and during oscillatio...
Text Solution
|
- In each of the four situations of column-I , a stretched string or an ...
Text Solution
|
- A source of sound of frequency 1000 Hzmoves to the right with a speed ...
Text Solution
|