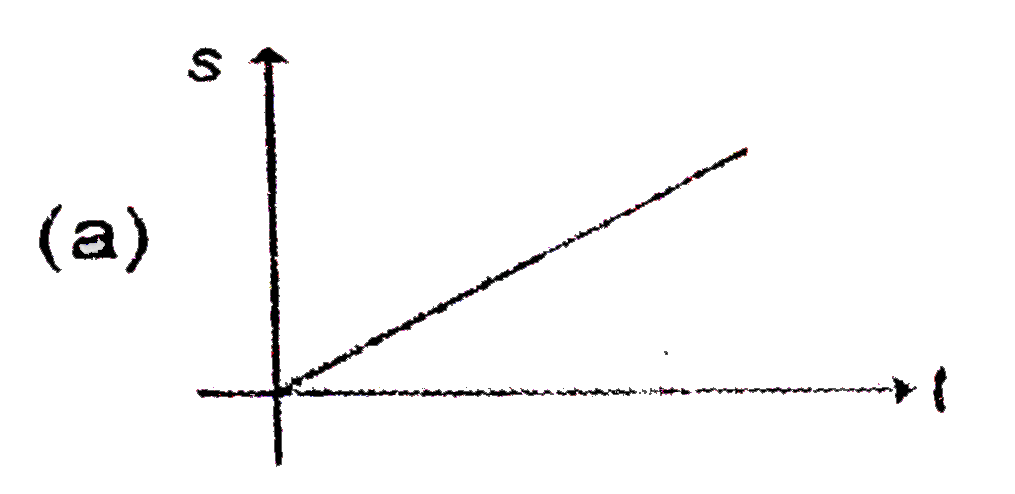
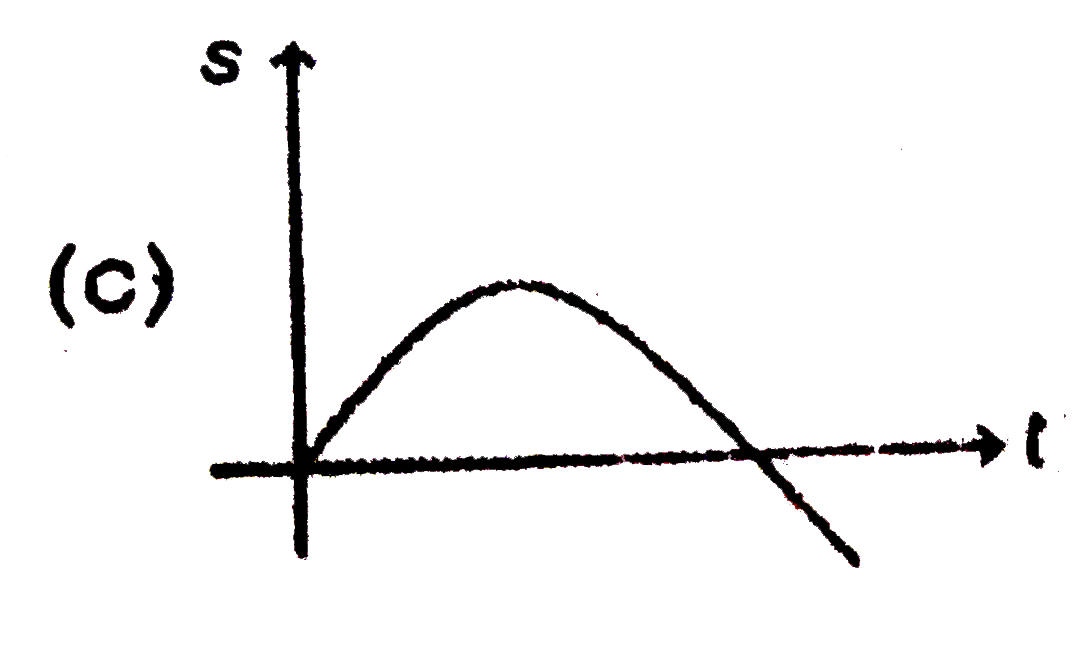
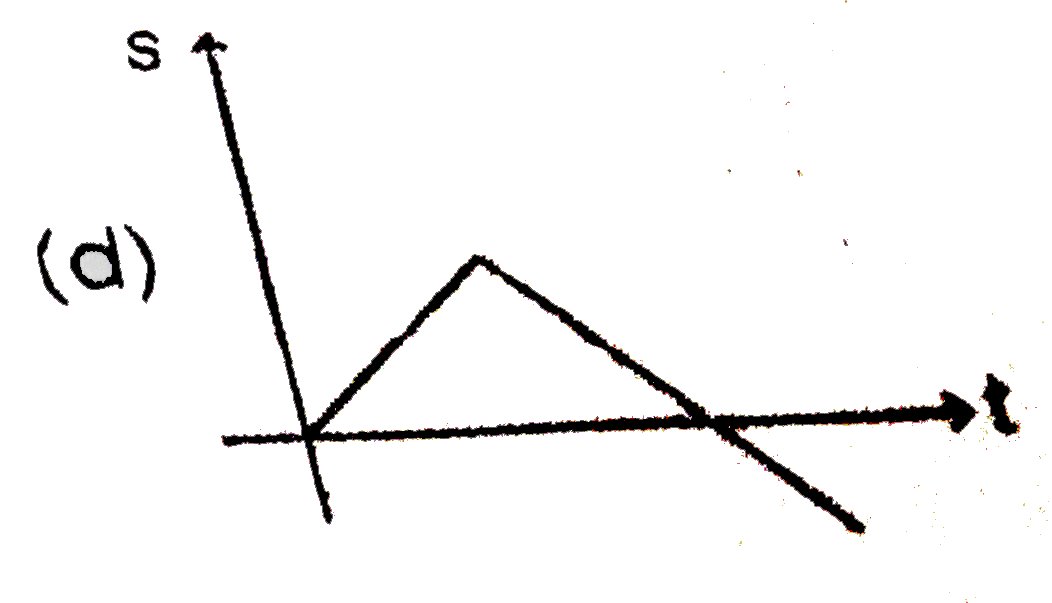
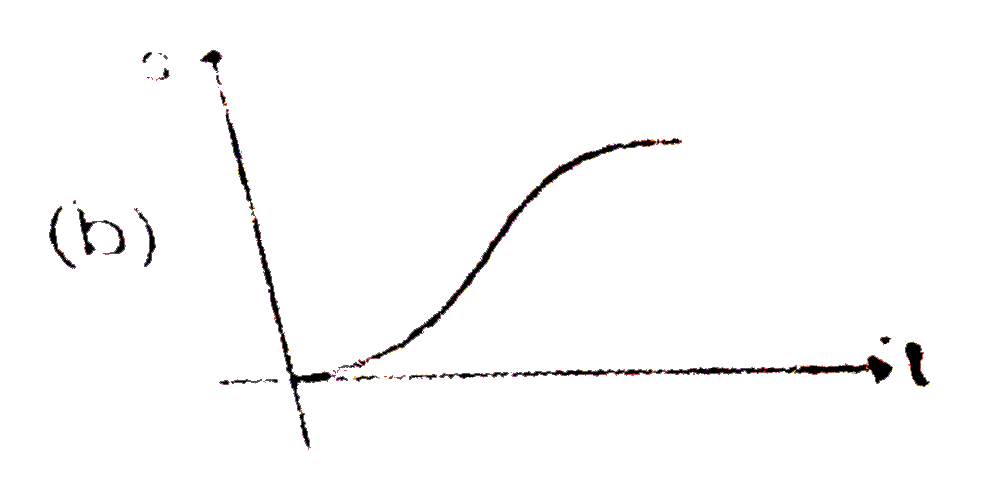A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-KINEMATICS 1-INTEGER_TYPE
- A particle is moving in x-y plane with y=x/2 and V(x)=4-2t. The displa...
Text Solution
|
- A stone is dropped from a certain height which can reach the ground in...
Text Solution
|
- A car starts moving along a line, first with acceleration a=5m//s^(2) ...
Text Solution
|
- Two particles P and Q simultaneously start moving from point A with ve...
Text Solution
|
- If a particle takes t second less and acquire a velocity of vms^(-1) m...
Text Solution
|
- Speed time graph of two cars A and B approaching towards each other is...
Text Solution
|
- The acceleration-time graph of a particle moving along a straight line...
Text Solution
|
- A lift performs the first part of its ascent with uniform acceleration...
Text Solution
|
- A small electric car has a maximum constant acceleration of 1m//s^(2),...
Text Solution
|
- The diagram shows the variatioin of 1//v (where v is velocity of the p...
Text Solution
|
- Two particles are moving with velocities v(1)=hati-thatj+hatk and v(2)...
Text Solution
|
- A particle A moves with velocity (2hati-3hatj)m//s from a point (4,5m)...
Text Solution
|
- A ball is thrown upwards with a speed of 40m//s. When the speed become...
Text Solution
|
- Figure shows the velocity time graph for a particle travelling along a...
Text Solution
|
- Two bodies A and B are moving along y-axis and x -axis as shown. Find ...
Text Solution
|
- The 1//v versus positions graph of a particle is shown in the figure, ...
Text Solution
|