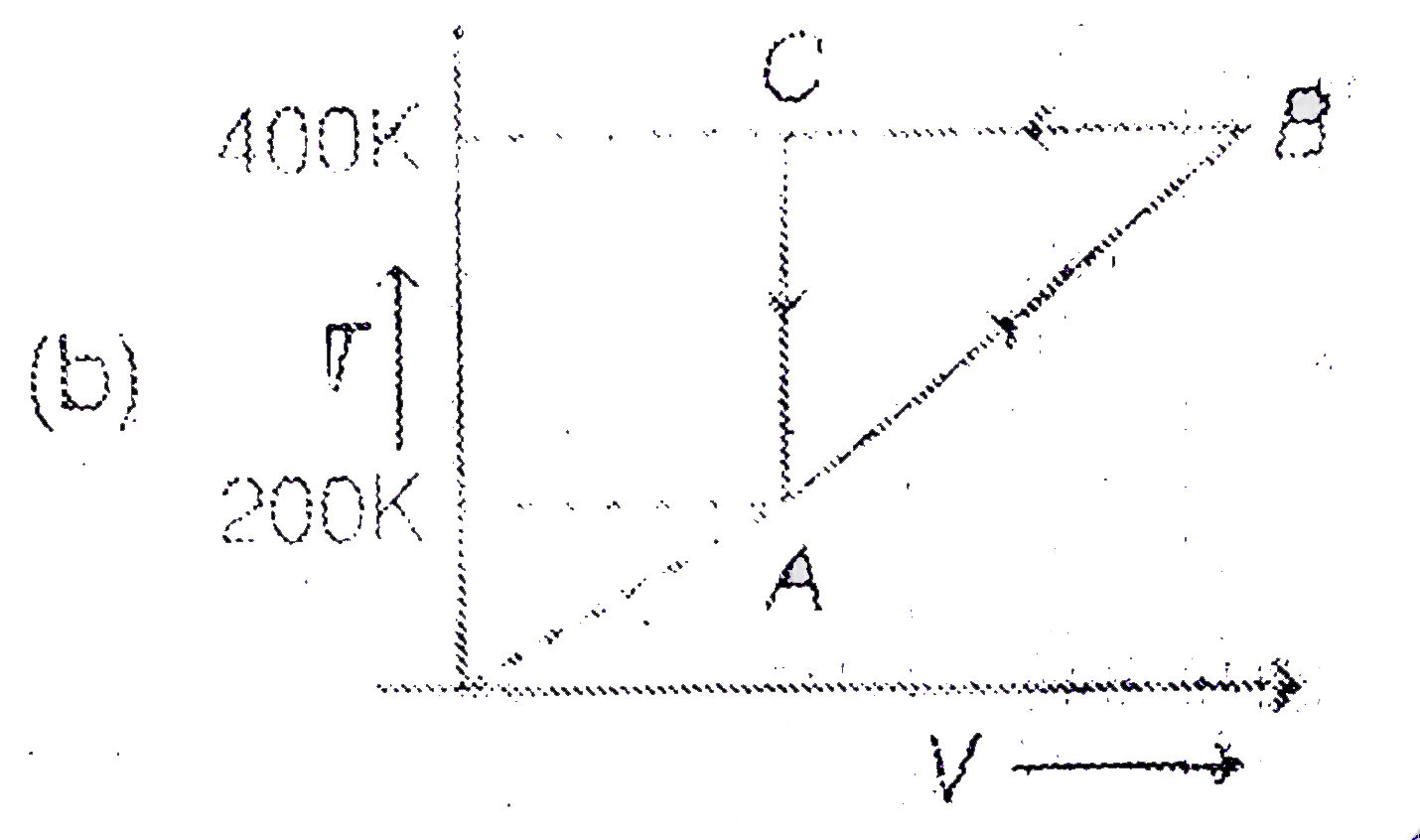
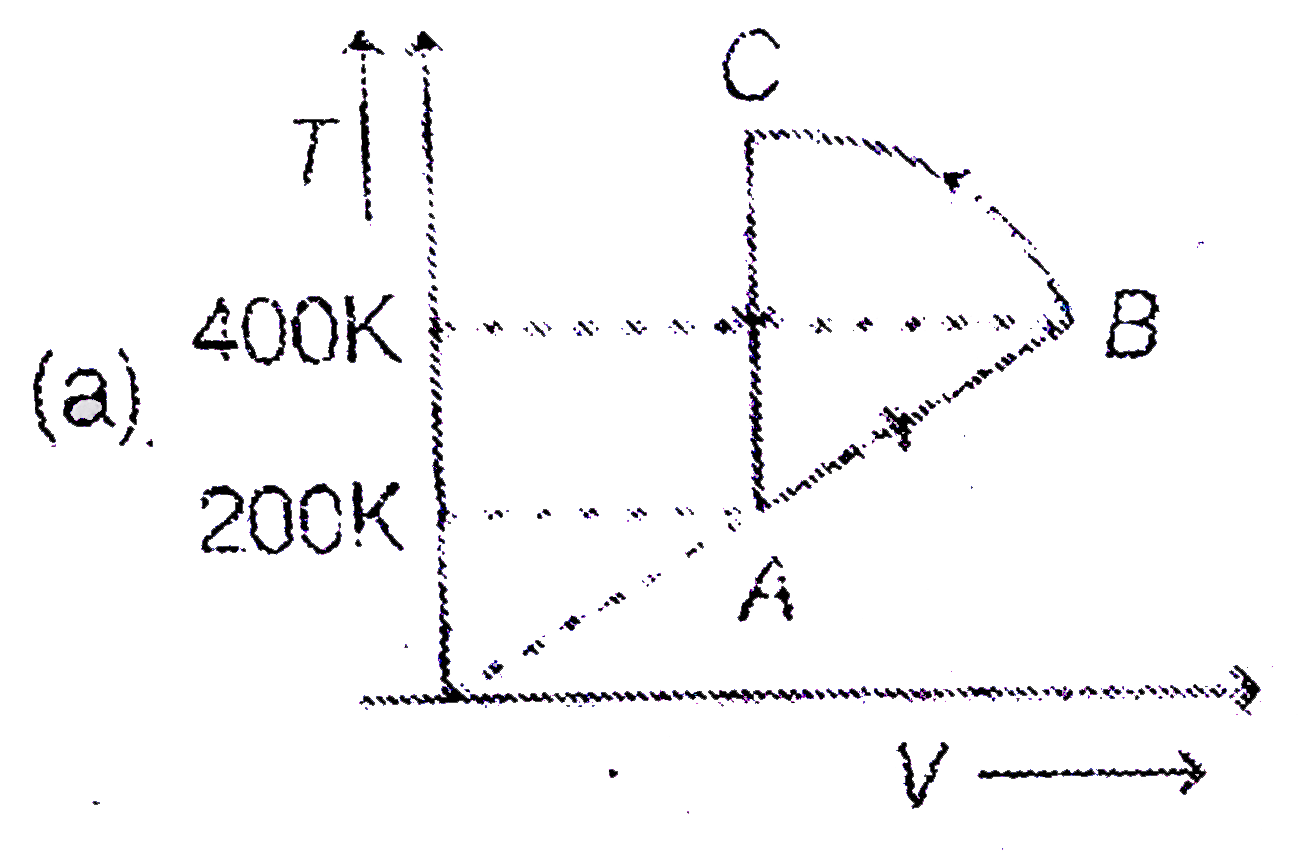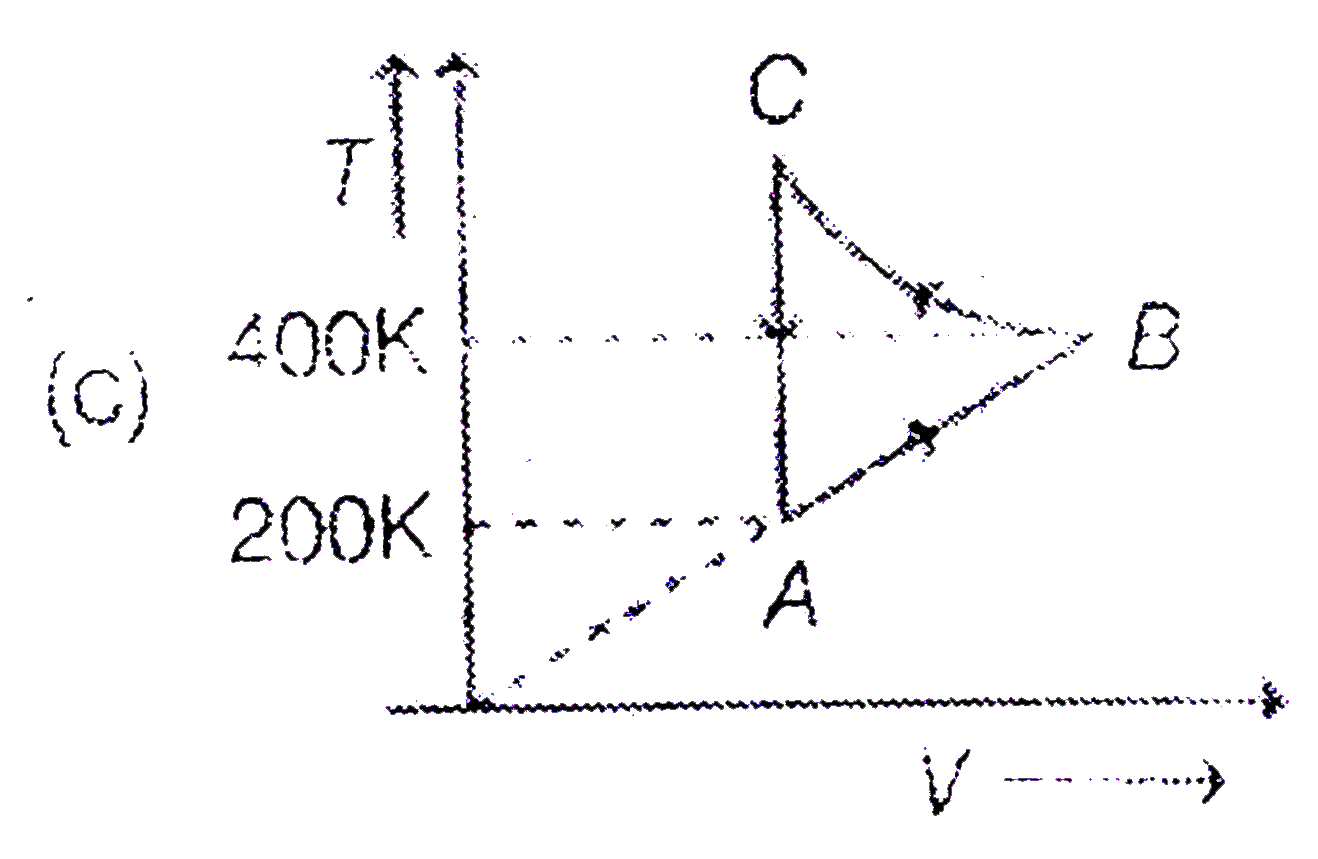A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-CURRENT ELECTRICITY-All Questions
- A metal block is placed in a room which is at 10^(@)C for long time. N...
Text Solution
|
- A metal block is placed in a room which is at 10^(@)C for long time. N...
Text Solution
|
- Four moles of an ideal gas is initially in a state A having pressure 2...
Text Solution
|
- Four moles of an ideal gas is initially in a state A having pressure 2...
Text Solution
|
- Two moles of a diatomic gas are carried trhough the cycle ABCDA as sho...
Text Solution
|
- Two moles of a diatomic gas are carried trhough the cycle ABCDA as sho...
Text Solution
|
- Two moles of a diatomic gas are carried trhough the cycle ABCDA as sho...
Text Solution
|
- 2 moles of an ideal monoatomic gas undergoes a cyclic process ABCA as ...
Text Solution
|
- 2 moles of an ideal monoatomic gas undergoes a cyclic process ABCA as ...
Text Solution
|
- 2 moles of an ideal monoatomic gas undergoes a cyclic process ABCA as ...
Text Solution
|
- One mole of helium gas follows the cycle 1-2-3-1 shown in the diagram....
Text Solution
|
- One mole of helium gas follows the cycle 1-2-3-1 shown in the diagram....
Text Solution
|
- Match the following
Text Solution
|
- In the rho-T graph shown in figure, match the following.
Text Solution
|
- In process Tprop(1)/(V), pressure of the gas increases from p(0) to 4p...
Text Solution
|
- Three liquids A, B and C having same specific heat and mass , 2m and 3...
Text Solution
|
- For a monoatomic gas at temperature T, match the following.
Text Solution
|
- Three rods of equal length of same material are joined to form an equi...
Text Solution
|
- Match the following.
Text Solution
|
- Match the following.
Text Solution
|