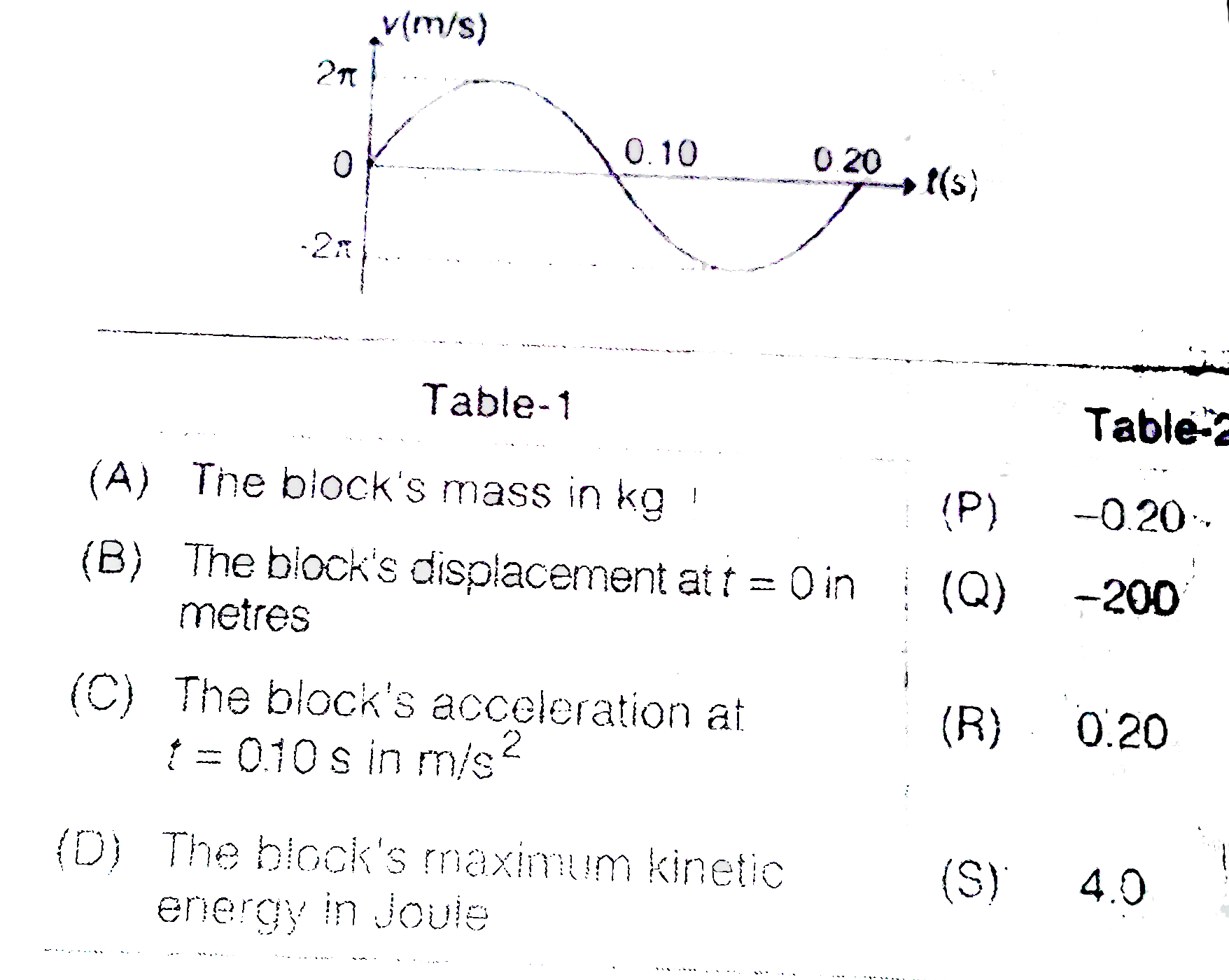Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
DC PANDEY ENGLISH|Exercise Integer type questions|14 VideosSIMPLE HARMONIC MOTION
DC PANDEY ENGLISH|Exercise Comprehension types|18 VideosSEMICONDUCTORS AND ELECTRONIC DEVICES
DC PANDEY ENGLISH|Exercise More than One Option is Correct|3 VideosSOLVD PAPERS 2017 NEET, AIIMS & JIPMER
DC PANDEY ENGLISH|Exercise Solved paper 2018(JIPMER)|38 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-SIMPLE HARMONIC MOTION-Matrix matching type questions
- In SHM, match the following.
Text Solution
|
- In the equation y=Asin(omegat+pi/4) match the following for x=A/2.
Text Solution
|
- In spring-block system match the following
Text Solution
|
- In y=A"sin"omegat + A"sin"(omegat=(2pi)/(3)), match the following.
Text Solution
|
- In SHM match the following
Text Solution
|
- Velocity-time graph of a particle in SHM is as shown in figure. Match ...
Text Solution
|
- A uniform rod of length l is suspended from a point P. and the rod is ...
Text Solution
|
- In the two block spring system, force constant of spring is k = 6N/m. ...
Text Solution
|
- In case of second's pendulum, match the following (consider shape of e...
Text Solution
|
- F-x and x-t graph of a principle in SHM are as shown in figure. Match ...
Text Solution
|
- x-t equation of a particle in SHM is given as x=1.0sin(12pit) in SI un...
Text Solution
|
- In a spring-block system, match the following:
Text Solution
|
- A simple harmonic oscillator consists of a block attached to a spring ...
Text Solution
|