Home
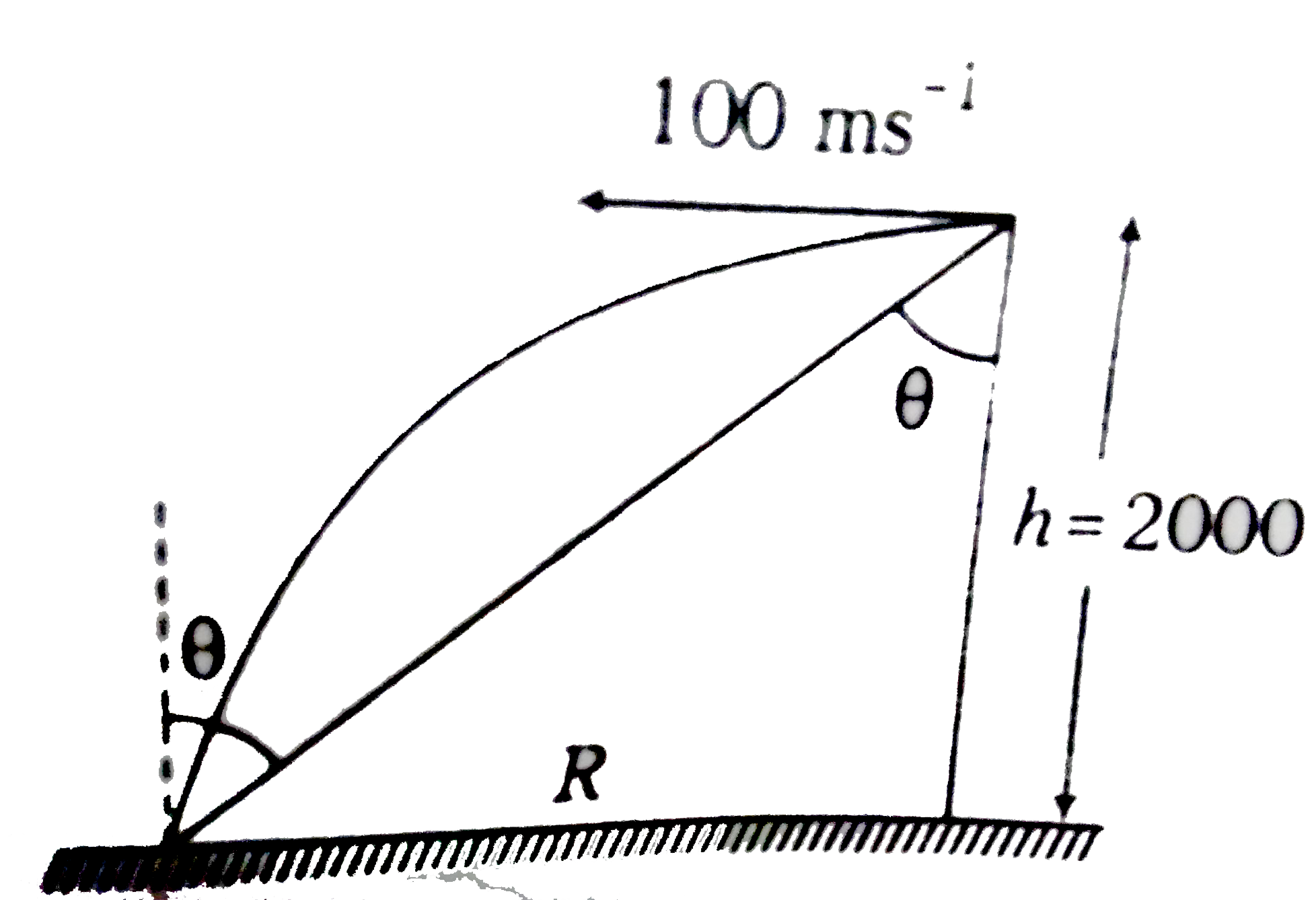
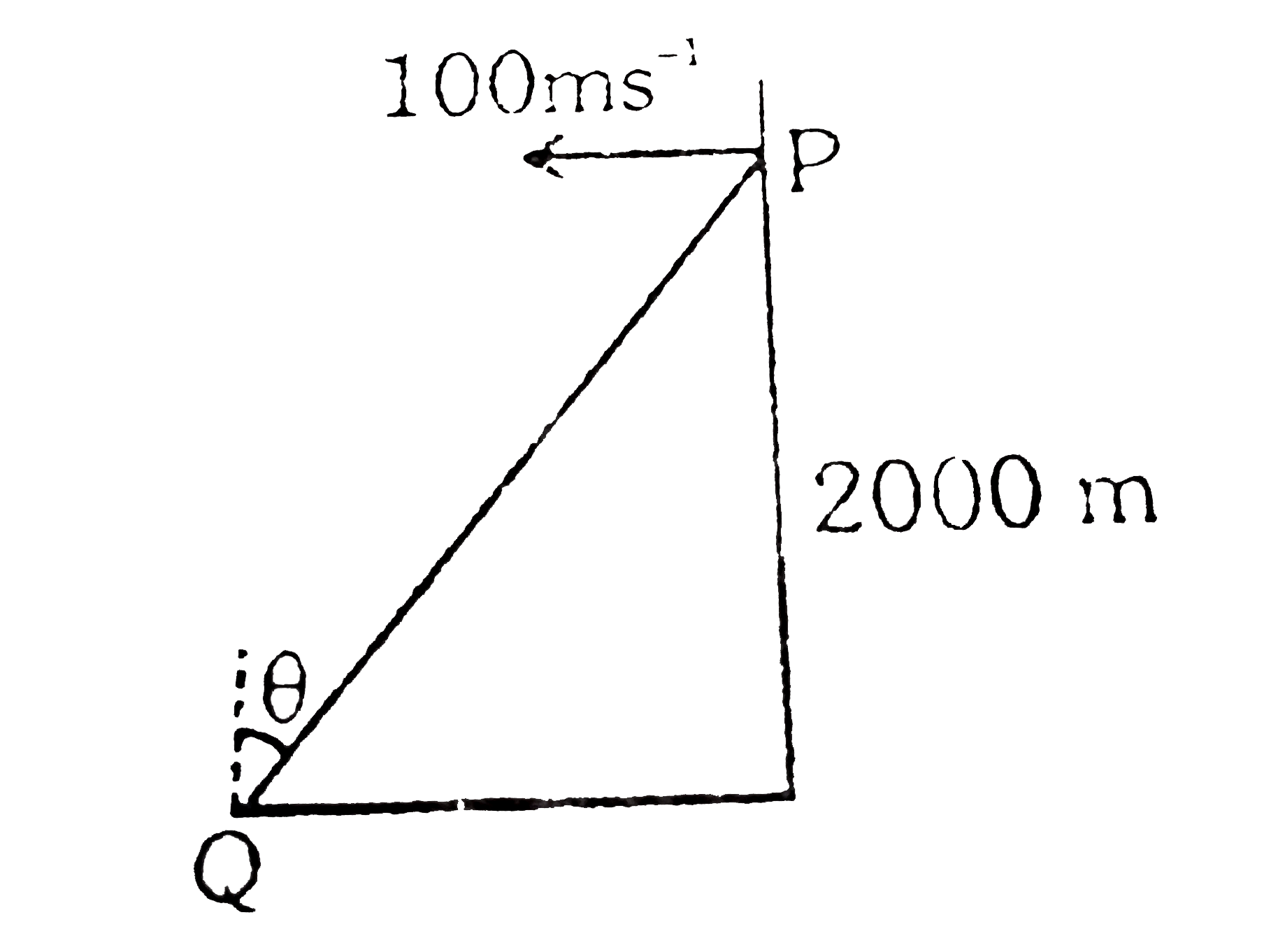Class 11
PHYSICS
An aeroplane is travelling at a height o...

An aeroplane is travelling at a height of 2000 m from the ground. The aeroplane, when at a point P, drops a bomb to hit a stationary target Q on the ground. In order that the bomb hits the target, what angle `theta` must the line PQ make with the vertical? `[g=10 ms^(-2)]`

A

`45^(@)`

B

`30^(@)`

C

`60^(@)`

D

`90^(@)`

Text Solution

Verified by Experts

The correct Answer is:
A
Let t be the time taken by bomb to hit the target.
`h = 2000 = (1)/(2) g t^(2) rArr t = 20s`

`R = ut = (100) (20) = 200m`
`:' tan theta = (R)/(h) = (2000)/(2000) = 1 rArr theta = 45^(@)`
Promotional Banner

Topper's Solved these Questions

  • MOTION

    DC PANDEY ENGLISH|Exercise A. Taking it together|1 Videos

  • MOTION

    DC PANDEY ENGLISH|Exercise Taking it together|96 Videos

  • MOTION

    DC PANDEY ENGLISH|Exercise Check Point 4.2|20 Videos

  • MEASUREMENT AND ERRORS

    DC PANDEY ENGLISH|Exercise Subjective|19 Videos

  • MOTION IN A PLANE

    DC PANDEY ENGLISH|Exercise (C )Medical entrances gallery|32 Videos

Similar Questions

Explore conceptually related problems

An aeroplane moving horizontally at a speed of 200 m//s and at a height of 8.0 xx 10^(3)m is to drop a bomb on a target. At what horizontal distance from the target should the bomb be released

An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60^@ and 45^@ respectively. Find the vertical distance between the aeroplanes at that instant.

An aeroplane flying horizontally at an altitude of 490m with a speed of 180 kmph drops a bomb. The horizontal distance at which it hits the ground is

An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60^0&45^0 respectively. Find the vertical distance between the aeroplanes at that instant.

A ball is dropped from a height of 45 m from the ground. The coefficient of restitution between the ball and the ground is 2/3 . What is the distance travelled by the ball in 4th second of its motion. Assume negligible time is spent in rebounding. Let g= 10 ms^(2)

An aeroplane flying horizontally with a speed of 360 km h^(-1) releases a bomb at a height of 490 m from the ground. If g = 9. 8 m s^(-2) , it will strike the ground at

A helicopter while flying at a height of 100 m with velocity 30 m.s at an angle 30^(@) with the horizontal, drops a packet. Where will the packet strike the ground ? ( g = 10 m//s^(2) )

A jet aeroplane is flying at a constant height of 2 km with a speed 360 kmh^(-1) above the ground towards a target and releases a bomb. After how much time it will hit the target and what will be the horizontal distance of the aeroplane from the target so that the bomb should hit the target ? (Take g = 10 ms^(-2))

A bomb is dropped on an enemy post by an aeroplane flying with a horizontal velocity of 60 km//hr and at a height of 490 m. How far the aeroplane must be from the enemy post at time of dropping the bomb, so that it may directly hit the target ? (g = 9.8 m//s^(2)). What is the trajectory of the bomb as seen by an observer on the earth? What as seen by a person sitting inside the aeroplane?

A rifle shoots a bullet with a muzzle velocity of 400 m s^-1 at a small target 400 m away. The height above the target at which the bullet must be aimed to hit the target is (g = 10 m s^-2) .